สามเหลี่ยมของแรงดัน ความต้านทาน และกำลัง

ใครก็ตามที่มีความคิดเกี่ยวกับไดอะแกรมเวกเตอร์จะสังเกตได้ง่ายว่ารูปสามเหลี่ยมแรงดันมุมฉากสามารถแยกแยะได้อย่างชัดเจนในแต่ละด้านซึ่งสะท้อนถึง: แรงดันรวมของวงจร, แรงดันของความต้านทานที่ใช้งานและแรงดัน เกี่ยวกับปฏิกิริยา.

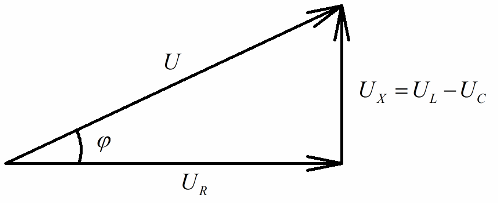
ตามทฤษฎีบทพีทาโกรัส ความสัมพันธ์ระหว่างแรงดันเหล่านี้ (ระหว่างแรงดันรวมของวงจรและแรงดันของส่วน) จะมีลักษณะดังนี้:

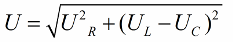
หากขั้นตอนต่อไปคือการแบ่งค่าของแรงดันเหล่านี้ด้วยกระแส (กระแสไหลผ่านทุกส่วนของวงจรอนุกรมเท่า ๆ กัน) จากนั้น กฎของโอห์ม เราได้ค่าความต้านทานนั่นคือตอนนี้เราสามารถพูดคุยเกี่ยวกับความต้านทานสามเหลี่ยมมุมฉาก:

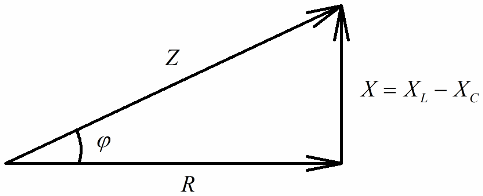
ในทำนองเดียวกัน (ในกรณีของแรงดันไฟฟ้า) การใช้ทฤษฎีบทพีทาโกรัส เป็นไปได้ที่จะสร้างความสัมพันธ์ระหว่างอิมพีแดนซ์ของวงจรและรีแอกแตนซ์ ความสัมพันธ์จะแสดงด้วยสูตรต่อไปนี้:

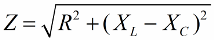
จากนั้นเราคูณค่าความต้านทานด้วยกระแส อันที่จริงเราจะเพิ่มแต่ละด้านของสามเหลี่ยมมุมฉากตามจำนวนครั้งที่กำหนด เป็นผลให้เราได้รูปสามเหลี่ยมมุมฉากที่มีความจุ:

พลังงานที่ใช้งานที่ปล่อยออกมาที่ความต้านทานที่ใช้งานของวงจรที่เกี่ยวข้องกับการแปลงพลังงานไฟฟ้ากลับไม่ได้ (เป็นความร้อนในการปฏิบัติงานในการติดตั้ง) จะเกี่ยวข้องอย่างชัดเจนกับพลังงานปฏิกิริยาที่เกี่ยวข้องกับการแปลงพลังงานแบบย้อนกลับ (การสร้าง ของสนามแม่เหล็กและสนามไฟฟ้าในขดลวดและตัวเก็บประจุ) และจ่ายไฟเต็มจำนวนให้กับการติดตั้งระบบไฟฟ้า

พลังงานที่ใช้งานวัดเป็นวัตต์ (W) พลังงานปฏิกิริยา — ในหน่วย varis (VAR — โวลต์-แอมแปร์รีแอกทีฟ) รวม — ใน VA (โวลต์-แอมแปร์)

ตามทฤษฎีบทพีทาโกรัส เรามีสิทธิที่จะเขียน:

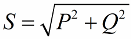
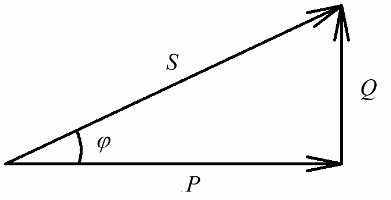
ตอนนี้ให้ความสนใจกับความจริงที่ว่าในสามเหลี่ยมกำลังมีมุม phi ซึ่งโคไซน์นั้นง่ายต่อการกำหนดโดยหลักจากกำลังที่ใช้งานและกำลังปรากฏ โคไซน์ของมุมนี้ (cos phi) เรียกว่าเพาเวอร์แฟกเตอร์ แสดงปริมาณพลังงานทั้งหมดที่ใช้เมื่อทำงานที่เป็นประโยชน์ในการติดตั้งระบบไฟฟ้าและไม่ได้ส่งคืนไปยังกริด

เห็นได้ชัดว่าตัวประกอบกำลังที่สูงขึ้น (สูงสุดหนึ่งตัว) บ่งชี้ถึงประสิทธิภาพการแปลงที่สูงขึ้นของพลังงานที่ส่งไปยังโรงงานเพื่อดำเนินการ หากตัวประกอบกำลังเป็น 1 พลังงานทั้งหมดที่ให้มาจะถูกใช้ในการทำงาน

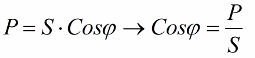
อัตราส่วนที่ได้รับช่วยให้สามารถแสดงปริมาณการใช้กระแสไฟฟ้าของการติดตั้งในแง่ของตัวประกอบกำลัง, กำลังไฟฟ้าที่ใช้งานและแรงดันไฟฟ้าของเครือข่าย:

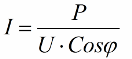
ดังนั้น ยิ่งโคไซน์พีมีขนาดเล็กเท่าใด เครือข่ายก็ต้องการกระแสมากขึ้นเพื่อทำงานบางอย่าง ในทางปฏิบัติ ปัจจัยนี้ (กระแสสูงสุดของเครือข่าย) จะจำกัดความสามารถในการรับส่งข้อมูลของสายส่ง ดังนั้น ยิ่งปัจจัยด้านพลังงานต่ำ โหลดของสายก็จะยิ่งมากขึ้น และแบนด์วิธที่มีประโยชน์ก็จะยิ่งน้อยลง (ค่า cosine phi ที่ต่ำจะนำไปสู่ข้อจำกัด ) การสูญเสียจูลในสายส่งไฟฟ้าโดยมีค่าโคไซน์ฟีลดลงสามารถดูได้จากสูตรต่อไปนี้:

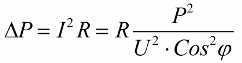
บนความต้านทานแอ็คทีฟ R ของสายส่ง ความสูญเสียจะเพิ่มมากขึ้นตามกระแส I ที่มากขึ้น แม้ว่าจะมีปฏิกิริยาต่อโหลดก็ตาม ดังนั้นเราจึงสามารถพูดได้ว่าด้วยตัวประกอบกำลังไฟฟ้าต่ำ ค่าใช้จ่ายในการส่งไฟฟ้าก็เพิ่มขึ้น ซึ่งหมายความว่าการเพิ่ม cosine phi เป็นภารกิจทางเศรษฐกิจระดับชาติที่สำคัญ

เป็นที่พึงปรารถนาว่าองค์ประกอบปฏิกิริยาของพลังงานทั้งหมดควรเข้าใกล้ศูนย์ ในการทำเช่นนี้ เป็นการดีที่จะใช้มอเตอร์ไฟฟ้าและหม้อแปลงไฟฟ้าที่โหลดเต็มที่เสมอ และปิดเมื่อสิ้นสุดการใช้งานเพื่อไม่ให้ไม่ได้ใช้งาน เมื่อไม่มีโหลด มอเตอร์และหม้อแปลงจะมีตัวประกอบกำลังที่ต่ำมาก วิธีหนึ่งในการเพิ่ม cosine phi ในผู้ใช้คือการใช้ ธนาคารตัวเก็บประจุ และ ตัวชดเชยแบบซิงโครนัส.