ตัวต้านทานและตัวเหนี่ยวนำในวงจรไฟฟ้ากระแสสลับ

การพิจารณาวงจรไฟฟ้ากระแสสลับที่มีความต้านทานแบบอุปนัยเท่านั้น (ดูบทความ «ตัวเหนี่ยวนำในวงจรไฟฟ้ากระแสสลับ») เราคิดว่าความต้านทานที่ใช้งานของวงจรนี้เป็นศูนย์

ในความเป็นจริงทั้งลวดของขดลวดและสายเชื่อมต่อมีความต้านทานเพียงเล็กน้อย แต่ใช้งานได้ดังนั้นวงจรจึงใช้พลังงานจากแหล่งกระแสอย่างหลีกเลี่ยงไม่ได้

ดังนั้นเมื่อพิจารณาค่าความต้านทานรวมของวงจรภายนอก จึงจำเป็นต้องเพิ่มค่าความต้านทานแบบรีแอคทีฟและแอคทีฟ แต่เป็นไปไม่ได้ที่จะเพิ่มความต้านทานทั้งสองนี้ซึ่งแตกต่างกันโดยธรรมชาติ

ในกรณีนี้ ความต้านทานของวงจรต่อไฟฟ้ากระแสสลับพบได้จากการบวกทางเรขาคณิต

มีการสร้างรูปสามเหลี่ยมมุมฉาก (ดูรูปที่ 1) ซึ่งด้านหนึ่งเป็นค่าของความต้านทานแบบเหนี่ยวนำ และอีกด้านหนึ่งคือค่าของความต้านทานแบบแอคทีฟ อิมพีแดนซ์ของวงจรที่ต้องการถูกกำหนดโดยด้านที่สามของรูปสามเหลี่ยม

รูปที่ 1 การหาค่าอิมพีแดนซ์ของวงจรที่มีความต้านทานแบบเหนี่ยวนำและแบบแอคทีฟ

ความต้านทานของวงจรแสดงด้วยตัวอักษรละติน Z และวัดเป็นโอห์ม จะเห็นได้จากโครงสร้างว่าความต้านทานรวมจะมากกว่าความต้านทานแบบอุปนัยและแบบแอคทีฟที่แยกจากกันเสมอ

การแสดงออกทางพีชคณิตสำหรับความต้านทานวงจรทั้งหมดคือ:

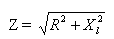
โดยที่ Z - ความต้านทานรวม, R - ความต้านทานที่ใช้งาน, XL - ความต้านทานอุปนัยของวงจร

ดังนั้นความต้านทานรวมของวงจรต่อกระแสสลับซึ่งประกอบด้วยความต้านทานแบบแอคทีฟและแบบเหนี่ยวนำจะเท่ากับรากที่สองของผลรวมของกำลังสองของความต้านทานแบบแอคทีฟและแบบเหนี่ยวนำของวงจรนี้

กฎของโอห์ม เนื่องจากวงจรดังกล่าวแสดงโดยสูตร I = U / Z โดยที่ Z คือความต้านทานรวมของวงจร

ให้เราวิเคราะห์ว่าแรงดันไฟฟ้าจะเป็นอย่างไรหากวงจรนอกเหนือจากและและการเปลี่ยนเฟสระหว่างกระแสและตัวเหนี่ยวนำยังมีความต้านทานที่ใช้งานอยู่ค่อนข้างมาก ในทางปฏิบัติ วงจรดังกล่าวสามารถเป็นได้ เช่น วงจรที่มีตัวเหนี่ยวนำแกนเหล็กพันด้วยลวดเส้นเล็ก (โช้คความถี่สูง)

ในกรณีนี้ การเปลี่ยนเฟสระหว่างกระแสและแรงดันจะไม่เท่ากับหนึ่งในสี่ของช่วงเวลาอีกต่อไป (เหมือนในวงจรที่มีความต้านทานแบบอุปนัยเท่านั้น) แต่จะน้อยกว่ามาก และยิ่งมีความต้านทานมากเท่าใดก็จะส่งผลให้การเลื่อนเฟสน้อยลงเท่านั้น

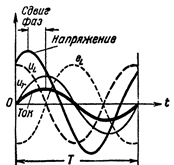
รูปที่ 2 กระแสและแรงดันในวงจรที่มี R และ L

ตอนนี้เธอเอง EMF ของการเหนี่ยวนำตัวเอง ไม่อยู่ในเฟสต้านกับแรงดันแหล่งจ่ายปัจจุบัน เนื่องจากมันถูกหักล้างด้วยความเคารพแรงดันไม่เกินครึ่งช่วง แต่น้อยกว่านอกจากนี้ แรงดันไฟฟ้าที่สร้างขึ้นโดยแหล่งกระแสที่ขั้วของขดลวดนั้นไม่เท่ากับแรงเคลื่อนไฟฟ้าของการเหนี่ยวนำตัวเอง แต่จะมีค่ามากกว่าแรงดันตกคร่อมในความต้านทานที่ใช้งานของขดลวด กล่าวอีกนัยหนึ่ง แรงดันไฟฟ้าในขดลวดประกอบด้วยสองส่วน:

• tiL- ส่วนประกอบปฏิกิริยาของแรงดันไฟฟ้าซึ่งปรับสมดุลของผลกระทบของ EMF จากการเหนี่ยวนำตัวเอง

• TiR- ส่วนประกอบที่ใช้งานของแรงดันไฟฟ้าที่จะเอาชนะความต้านทานที่ใช้งานของวงจร

หากเราเชื่อมต่อความต้านทานแบบแอคทีฟขนาดใหญ่เป็นอนุกรมกับขดลวด การเลื่อนเฟสจะลดลงมากจนคลื่นไซน์ปัจจุบันเกือบจะตามทันกับคลื่นไซน์ของแรงดันและความแตกต่างของเฟสระหว่างพวกมันจะแทบไม่สังเกตเห็นได้ ในกรณีนี้ แอมพลิจูดของเทอมและจะมากกว่าแอมพลิจูดของเทอม

ในทำนองเดียวกัน คุณสามารถลดการเปลี่ยนเฟสและแม้แต่ลดให้เหลือศูนย์ได้อย่างสมบูรณ์หากคุณลดความถี่ของเครื่องกำเนิดไฟฟ้าไม่ทางใดก็ทางหนึ่ง ความถี่ที่ลดลงจะส่งผลให้ EMF เหนี่ยวนำตัวเองลดลง ดังนั้นการเลื่อนเฟสระหว่างกระแสและแรงดันในวงจรจึงลดลง

กำลังของวงจรไฟฟ้ากระแสสลับที่มีตัวเหนี่ยวนำ

วงจรไฟฟ้ากระแสสลับที่มีขดลวดไม่ใช้พลังงานของแหล่งกระแส และในวงจรมีกระบวนการแลกเปลี่ยนพลังงานระหว่างเครื่องกำเนิดไฟฟ้าและวงจร

ตอนนี้ให้เราวิเคราะห์ว่าสิ่งต่าง ๆ จะเป็นอย่างไรกับพลังงานที่ใช้โดยโครงการดังกล่าว

พลังงานที่ใช้ในวงจรไฟฟ้ากระแสสลับมีค่าเท่ากับผลคูณของกระแสและแรงดัน แต่เนื่องจากกระแสและแรงดันเป็นปริมาณที่ผันแปร ดังนั้นกำลังไฟฟ้าจึงแปรผันตามไปด้วยในกรณีนี้ เราสามารถกำหนดค่าพลังงานสำหรับแต่ละช่วงเวลาได้หากเราคูณค่าปัจจุบันด้วยค่าแรงดันไฟฟ้าที่สอดคล้องกับช่วงเวลาที่กำหนด

เพื่อให้ได้กราฟพลังงาน เราจำเป็นต้องคูณค่าของส่วนของเส้นตรงที่กำหนดกระแสและแรงดันในเวลาต่างๆ การก่อสร้างดังกล่าวแสดงในรูปที่ 3, ก. รูปคลื่นเส้นประ p แสดงให้เราเห็นว่าการเปลี่ยนแปลงของพลังงานในวงจรไฟฟ้ากระแสสลับที่มีความต้านทานแบบอุปนัยเท่านั้น

กฎการคูณพีชคณิตต่อไปนี้ใช้ในการสร้างเส้นโค้งนี้: เมื่อค่าบวกคูณด้วยค่าลบ จะได้ค่าลบ และเมื่อคูณค่าลบสองค่าหรือค่าบวกสองค่า จะได้ค่าบวก

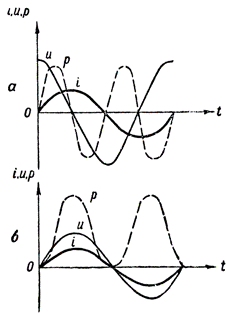
รูปที่ 3 กราฟพลังงาน: a — ในวงจรที่มีความต้านทานแบบเหนี่ยวนำ b — รวมถึงความต้านทานแบบแอคทีฟ

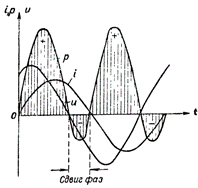
รูปที่ 4 ผังกำลังสำหรับวงจรที่มี R และ L

เส้นกำลังในกรณีนี้อยู่เหนือแกนเวลา ซึ่งหมายความว่าไม่มีการแลกเปลี่ยนพลังงานระหว่างเครื่องกำเนิดไฟฟ้าและวงจร ดังนั้นพลังงานที่จ่ายโดยเครื่องกำเนิดไฟฟ้าไปยังวงจรจะถูกใช้โดยวงจรทั้งหมด

ในรูป 4 แสดงผังกำลังสำหรับวงจรที่มีทั้งความต้านทานแบบเหนี่ยวนำและแบบแอ็คทีฟ ในกรณีนี้ การถ่ายโอนพลังงานย้อนกลับจากวงจรไปยังแหล่งกระแสก็เกิดขึ้นเช่นกัน แต่ในระดับที่น้อยกว่าในวงจรที่มีความต้านทานแบบอุปนัยเดียว

หลังจากตรวจสอบกราฟพลังงานข้างต้นแล้ว เราสรุปว่าเฉพาะการเลื่อนเฟสระหว่างกระแสและแรงดันในวงจรเท่านั้นที่สร้างพลังงาน "ลบ"ในกรณีนี้ ยิ่งการเลื่อนเฟสระหว่างกระแสและแรงดันในวงจรมากขึ้น วงจรก็จะใช้พลังงานน้อยลง และในทางกลับกัน ยิ่งการเลื่อนเฟสน้อยลง วงจรก็จะยิ่งใช้พลังงานมากขึ้นเท่านั้น

อ่านเพิ่มเติม: เรโซแนนซ์แรงดันไฟฟ้าคืออะไร