แหล่งจ่ายไฟ AC และการสูญเสียพลังงาน

พลังของวงจรที่มีตัวต้านทานแบบแอคทีฟเท่านั้นเรียกว่า พลังแบบแอคทีฟ P ซึ่งคำนวณตามปกติโดยใช้สูตรใดสูตรหนึ่งต่อไปนี้:

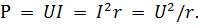
พลังงานที่ใช้งานอยู่แสดงถึงการใช้พลังงานในปัจจุบันที่ไม่สามารถย้อนกลับได้ (ไม่สามารถย้อนกลับได้)

ล่ามโซ่ กระแสสลับ มีหลายสาเหตุที่ทำให้เกิดการสูญเสียพลังงานที่ไม่สามารถกู้คืนได้มากกว่าในวงจรไฟฟ้ากระแสตรง เหตุผลเหล่านี้มีดังนี้:

1. การทำให้ลวดร้อนด้วยกระแสไฟฟ้า… สำหรับไฟฟ้ากระแสตรง การให้ความร้อนแทบจะเป็นรูปแบบเดียวของการสูญเสียพลังงาน และสำหรับกระแสสลับซึ่งมีค่าเท่ากันกับกระแสตรง การสูญเสียพลังงานเพื่อให้ความร้อนแก่ลวดจะมากขึ้นเนื่องจากความต้านทานของลวดเพิ่มขึ้นเนื่องจากผลกระทบที่พื้นผิว ที่สูงกว่า ความถี่ปัจจุบันก็ยิ่งส่งผลกระทบมากขึ้นเท่านั้น ผลกระทบพื้นผิว และสูญเสียความร้อนลวดมากขึ้น

2. การสูญเสียเพื่อสร้างกระแสไหลวนหรือที่เรียกว่ากระแส Foucault… กระแสเหล่านี้ถูกเหนี่ยวนำในตัวโลหะทั้งหมดในสนามแม่เหล็กที่เกิดจากกระแสสลับ จากการกระทำ กระแสน้ำวน ตัวโลหะร้อนขึ้นการสูญเสียกระแสไหลวนที่มีนัยสำคัญโดยเฉพาะอย่างยิ่งสามารถสังเกตได้ในแกนเหล็ก การสูญเสียพลังงานเพื่อสร้างกระแสน้ำวนจะเพิ่มขึ้นตามความถี่ที่เพิ่มขึ้น

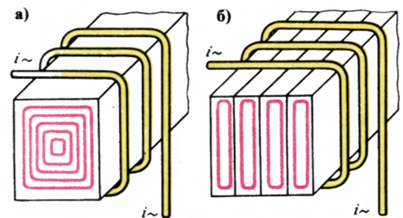
กระแสน้ำวน — ในแกนกลางขนาดใหญ่, b — ในแกนกลางแบบลาเมลลาร์

3. การสูญเสียฮิสเทรีซิสแม่เหล็ก... ภายใต้อิทธิพลของสนามแม่เหล็กสลับ แกนเฟอร์โรแมกเนติกจะถูกทำให้เป็นแม่เหล็กใหม่ ในกรณีนี้เกิดการเสียดสีกันของอนุภาคแกนกลางซึ่งเป็นผลมาจากการที่แกนกลางร้อนขึ้น เมื่อความถี่เพิ่มขึ้นการสูญเสียจาก ฮิสเทรีซิสแม่เหล็ก กำลังเติบโต

4. การสูญเสียในไดอิเล็กตริกที่เป็นของแข็งหรือของเหลว... ในไดอิเล็กตริกดังกล่าว ทำให้เกิดสนามไฟฟ้ากระแสสลับ โพลาไรเซชันของโมเลกุลนั่นคือประจุปรากฏที่ด้านตรงข้ามของโมเลกุล มีค่าเท่ากัน แต่มีเครื่องหมายต่างกัน โมเลกุลโพลาไรซ์จะหมุนภายใต้การกระทำของสนามและสัมผัสกับแรงเสียดทานซึ่งกันและกัน ด้วยเหตุนี้อิเล็กทริกจึงร้อนขึ้น เมื่อความถี่เพิ่มขึ้น ความสูญเสียก็เพิ่มขึ้น

5. การสูญเสียการรั่วไหลของฉนวน… สารฉนวนที่ใช้ไม่ใช่ไดอิเล็กตริกในอุดมคติและพบการรั่วไหลในตัว กล่าวอีกนัยหนึ่งความต้านทานของฉนวนแม้ว่าจะสูงมาก แต่ก็ไม่เท่ากับอนันต์ การสูญเสียประเภทนี้ยังมีอยู่ในกระแสตรง ที่แรงดันไฟฟ้าสูง เป็นไปได้ที่ประจุจะไหลไปในอากาศรอบๆ สาย

6. การสูญเสียเนื่องจากการแผ่รังสีของคลื่นแม่เหล็กไฟฟ้า… สายไฟ AC ใดๆ ปล่อยคลื่นแม่เหล็กไฟฟ้าและเมื่อความถี่เพิ่มขึ้น พลังงานของคลื่นที่ปล่อยออกมาจะเพิ่มขึ้นอย่างรวดเร็ว (เป็นสัดส่วนกับกำลังสองของความถี่)คลื่นแม่เหล็กไฟฟ้าออกจากตัวนำอย่างไม่สามารถย้อนกลับได้ ดังนั้นการใช้พลังงานสำหรับการปล่อยคลื่นจึงเทียบเท่ากับการสูญเสียในการต้านทานแบบแอคทีฟบางตัว ในเสาอากาศของเครื่องส่งสัญญาณวิทยุ การสูญเสียประเภทนี้เป็นการสูญเสียพลังงานที่มีประโยชน์

7. การสูญเสียกำลังส่งไปยังวงจรอื่น... ปรากฏการณ์ของการเหนี่ยวนำแม่เหล็กไฟฟ้า ไฟฟ้ากระแสสลับบางส่วนถูกถ่ายโอนจากวงจรหนึ่งไปยังอีกวงจรหนึ่งที่อยู่ใกล้เคียง ในบางกรณี เช่น ในหม้อแปลง การถ่ายโอนพลังงานนี้มีประโยชน์

ความต้านทานแบบแอกทีฟของวงจรไฟฟ้ากระแสสลับจะคำนึงถึงการสูญเสียพลังงานที่ไม่สามารถกู้คืนได้ทุกประเภทที่ระบุไว้ สำหรับวงจรอนุกรม คุณสามารถกำหนดความต้านทานแบบแอกทีฟเป็นอัตราส่วนของกำลังไฟฟ้า ความแรงของการสูญเสียทั้งหมดต่อกำลังสองของ ปัจจุบัน:

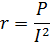
ดังนั้นสำหรับกระแสที่กำหนด ความต้านทานที่ใช้งานของวงจรจะยิ่งมากขึ้น กำลังไฟฟ้าที่ใช้งานก็จะยิ่งมากขึ้น นั่นคือการสูญเสียพลังงานทั้งหมดก็จะยิ่งมากขึ้นเท่านั้น

พลังงานในส่วนวงจรที่มีความต้านทานอุปนัยเรียกว่า พลังงานปฏิกิริยา ถาม... มันแสดงลักษณะของพลังงานปฏิกิริยา นั่นคือ พลังงานที่ไม่ได้ถูกใช้ไปอย่างถาวร แต่จะถูกเก็บไว้ชั่วคราวในสนามแม่เหล็กเท่านั้น เพื่อแยกความแตกต่างจากพลังงานที่ใช้งานอยู่ พลังงานปฏิกิริยาไม่ได้วัดเป็นวัตต์ แต่เป็นโวลต์แอมแปร์ปฏิกิริยา (var หรือ var)... ในแง่นี้ ก่อนหน้านี้เรียกว่าแอนไฮดรัส

พลังงานปฏิกิริยาถูกกำหนดโดยหนึ่งในสูตร:

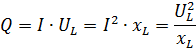
โดยที่ UL คือแรงดันไฟฟ้าในส่วนที่มีความต้านทานแบบเหนี่ยวนำ xL ฉันเป็นปัจจุบันในส่วนนี้

สำหรับวงจรอนุกรมที่มีความต้านทานแบบแอกทีฟและอุปนัย แนวคิดของกำลังรวม S ถูกนำมาใช้... ซึ่งจะถูกกำหนดโดยผลคูณของแรงดันรวมของวงจร U และกระแส I และแสดงเป็นโวลต์-แอมแปร์ (VA หรือ VA)

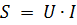
พลังงานในส่วนที่มีความต้านทานที่ใช้งานคำนวณโดยหนึ่งในสูตรด้านบนหรือตามสูตร:

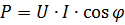
โดยที่ φ คือมุมเฟสระหว่างแรงดัน U และกระแส I

ค่าสัมประสิทธิ์ของ cosφ คือตัวประกอบกำลัง… มักถูกเรียกว่า «โคไซน์พี»… ตัวประกอบกำลังแสดงจำนวนกำลังไฟฟ้าทั้งหมดเป็นกำลังที่ใช้งานอยู่:

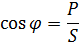
ค่าของ cosφ สามารถเปลี่ยนแปลงได้ตั้งแต่ศูนย์จนถึงเอกภาพ ขึ้นอยู่กับอัตราส่วนระหว่างความต้านทานแบบแอคทีฟและปฏิกิริยา หากมีเพียงหนึ่งเดียวในวงจร ปฏิกิริยาแล้ว φ = 90 °, cosφ = 0, P = 0 และพลังงานในวงจรนั้นเป็นปฏิกิริยาล้วน หากมีเพียงความต้านทานที่ใช้งานอยู่เท่านั้น φ = 0, cosφ = 1 และ P = S นั่นคือพลังงานทั้งหมดในวงจรจะทำงานอย่างหมดจด

ยิ่ง cosφ ต่ำ ส่วนแบ่งพลังงานที่ใช้งานของพลังงานปรากฏก็จะยิ่งน้อยลง และพลังงานปฏิกิริยาก็จะยิ่งสูงขึ้น แต่การทำงานของกระแสนั่นคือการเปลี่ยนพลังงานเป็นพลังงานประเภทอื่นนั้นมีลักษณะเฉพาะคือพลังงานที่ใช้งานอยู่ และพลังงานปฏิกิริยาจะกำหนดลักษณะของพลังงานที่ผันผวนระหว่างเครื่องกำเนิดและส่วนปฏิกิริยาของวงจร

สำหรับกริดไฟฟ้านั้นไร้ประโยชน์และเป็นอันตรายด้วยซ้ำ ควรสังเกตว่าในวิศวกรรมวิทยุ พลังงานปฏิกิริยามีความจำเป็นและมีประโยชน์ในหลายกรณี ตัวอย่างเช่น ในวงจรสั่นซึ่งใช้กันอย่างแพร่หลายในวิศวกรรมวิทยุและใช้ในการสร้างการสั่นทางไฟฟ้า ความแรงของการสั่นเหล่านี้เกือบจะเป็นปฏิกิริยาล้วนๆ
แผนภาพเวกเตอร์แสดงให้เห็นว่าการเปลี่ยนแปลงcosφเปลี่ยนตัวรับปัจจุบัน I โดยกำลังไม่เปลี่ยนแปลงอย่างไร

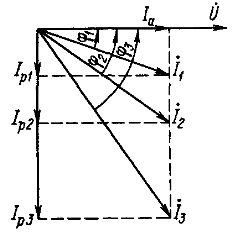
แผนภาพเวกเตอร์ของกระแสรับที่กำลังคงที่และตัวประกอบกำลังต่างๆ

ดังที่เห็นได้ ตัวประกอบกำลัง cosφ เป็นตัวบ่งชี้ที่สำคัญของระดับการใช้พลังงานทั้งหมดที่พัฒนาโดยเครื่องกำเนิด EMF แบบสลับ... จำเป็นต้องให้ความสนใจเป็นพิเศษกับข้อเท็จจริงที่ว่าที่ cosφ <1 เครื่องกำเนิดจะต้องสร้าง แรงดันและกระแสที่มีผลิตภัณฑ์มากกว่าพลังงานที่ใช้งานอยู่ ตัวอย่างเช่น หากพลังงานที่ใช้งานอยู่ในเครือข่ายไฟฟ้าคือ 1,000 kW และ cosφ = 0.8 ดังนั้นพลังงานที่ปรากฏจะเท่ากับ:

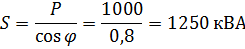
สมมติว่าในกรณีนี้ได้กำลังไฟฟ้าจริงที่แรงดัน 100 kV และกระแส 10 A อย่างไรก็ตาม เครื่องกำเนิดไฟฟ้าต้องสร้างแรงดัน 125 kV เพื่อให้กำลังไฟฟ้าปรากฏ

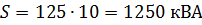
เป็นที่ชัดเจนว่าการใช้เครื่องกำเนิดไฟฟ้าสำหรับแรงดันไฟฟ้าที่สูงกว่านั้นเสียเปรียบ และยิ่งไปกว่านั้น ที่แรงดันไฟฟ้าที่สูงกว่านั้นจำเป็นต้องปรับปรุงฉนวนของสายไฟเพื่อหลีกเลี่ยงการรั่วไหลหรือการเกิดความเสียหายที่เพิ่มขึ้น สิ่งนี้จะนำไปสู่การเพิ่มราคาของกริดไฟฟ้า

ความจำเป็นในการเพิ่มแรงดันไฟฟ้าของเครื่องกำเนิดไฟฟ้าเนื่องจากการมีพลังงานปฏิกิริยาเป็นลักษณะของวงจรอนุกรมที่มีความต้านทานแบบแอคทีฟและรีแอคทีฟ หากมีวงจรคู่ขนานที่มีสาขาแอคทีฟและรีแอคทีฟ เครื่องกำเนิดไฟฟ้าจะต้องสร้างกระแสมากกว่าที่จำเป็นด้วยความต้านทานแบบแอคทีฟเดียว กล่าวอีกนัยหนึ่ง เครื่องกำเนิดไฟฟ้าจะโหลดด้วยกระแสรีแอกทีฟเพิ่มเติม

ตัวอย่างเช่นสำหรับค่าข้างต้น P = 1,000 kW, cosφ = 0.8 และ S = 1250 kVA เมื่อเชื่อมต่อแบบขนานเครื่องกำเนิดไฟฟ้าควรให้กระแสไม่ใช่ 10 A แต่ 12.5 A ที่แรงดัน 100 kV .ในกรณีนี้ ไม่เพียงแต่เครื่องกำเนิดไฟฟ้าจะต้องได้รับการออกแบบสำหรับกระแสไฟฟ้าที่มากขึ้นเท่านั้น แต่สายไฟของสายไฟฟ้าที่จะส่งผ่านกระแสไฟฟ้านี้จะต้องมีความหนามากขึ้น ซึ่งจะทำให้ต้นทุนต่อเส้นเพิ่มขึ้นด้วย หากในสายไฟและที่ขดลวดของเครื่องกำเนิดไฟฟ้ามีสายไฟที่ออกแบบมาสำหรับกระแส 10 A เป็นที่ชัดเจนว่ากระแส 12.5 A จะทำให้สายไฟเหล่านี้ร้อนขึ้น

ดังนั้นแม้ว่าการเสริม กระแสปฏิกิริยา ถ่ายโอนพลังงานปฏิกิริยาจากเครื่องกำเนิดไฟฟ้าไปยังโหลดปฏิกิริยาและในทางกลับกัน แต่สร้างการสูญเสียพลังงานที่ไม่จำเป็นเนื่องจากความต้านทานของสายไฟ

ในเครือข่ายไฟฟ้าที่มีอยู่ ส่วนที่มีความต้านทานปฏิกิริยาสามารถเชื่อมต่อได้ทั้งแบบอนุกรมและแบบขนานกับส่วนที่มีความต้านทานแบบแอคทีฟ ดังนั้นเครื่องกำเนิดไฟฟ้าจึงต้องพัฒนาแรงดันไฟและกระแสไฟเพิ่มขึ้นเพื่อสร้างพลังงานรีแอกทีฟที่มีประโยชน์ นอกเหนือจากพลังงานปฏิกิริยา

จากสิ่งที่ได้กล่าวมา เป็นที่ชัดเจนว่าการใช้พลังงานไฟฟ้ามีความสำคัญเพียงใด การเพิ่มค่าcosφ… การลดลงเกิดจากการรวมโหลดปฏิกิริยาในเครือข่ายไฟฟ้า ตัวอย่างเช่น มอเตอร์ไฟฟ้าหรือหม้อแปลงไฟฟ้าที่ไม่ได้ใช้งานหรือโหลดไม่เต็มที่จะสร้างโหลดรีแอกทีฟที่มีนัยสำคัญ เนื่องจากพวกมันมีความเหนี่ยวนำของขดลวดที่ค่อนข้างสูง ในการเพิ่ม cosφ สิ่งสำคัญคือมอเตอร์และหม้อแปลงต้องทำงานที่โหลดเต็มที่ มันมีอยู่ หลายวิธีในการเพิ่ม cosφ.

โดยสรุป เราทราบว่ากองกำลังทั้งสามเชื่อมโยงกันด้วยความสัมพันธ์ดังต่อไปนี้:

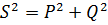
นั่นคือ พลังงานปรากฏไม่ใช่ผลรวมทางคณิตศาสตร์ของพลังงานเชิงรุกและเชิงปฏิกิริยาเป็นเรื่องปกติที่จะบอกว่ากำลัง S เป็นผลรวมทางเรขาคณิตของกำลัง P และ Q

ดูสิ่งนี้ด้วย: รีแอกแตนซ์ในวิศวกรรมไฟฟ้า