ความต้านทานภายในคืออะไร

สมมติว่ามีวงจรปิดทางไฟฟ้าอย่างง่ายที่มีแหล่งกำเนิดกระแส เช่น เครื่องกำเนิดไฟฟ้า เซลล์กัลวานิกหรือแบตเตอรี่ และตัวต้านทาน R เนื่องจากกระแสในวงจรจะไม่ถูกขัดจังหวะที่ใด กระแสจึงไหลภายในแหล่งกำเนิดด้วย

ในสถานการณ์เช่นนี้ เราสามารถพูดได้ว่าแต่ละแหล่งมีความต้านทานภายในที่ป้องกันไม่ให้กระแสไหล ความต้านทานภายในนี้แสดงลักษณะของแหล่งที่มาปัจจุบันและเขียนแทนด้วยตัวอักษร r สำหรับ เซลล์กัลวานิก หรือแบตเตอรี่ ความต้านทานภายในคือความต้านทานของสารละลายอิเล็กโทรไลต์และอิเล็กโทรด สำหรับเครื่องกำเนิดไฟฟ้า - ความต้านทานของขดลวดสเตเตอร์ เป็นต้น

ดังนั้น แหล่งกำเนิดกระแสจึงมีคุณลักษณะทั้งขนาดของ EMF และค่าของความต้านทานภายในของมันเอง r — คุณลักษณะทั้งสองบ่งบอกถึงคุณภาพของแหล่งที่มา

เครื่องกำเนิดไฟฟ้าสถิตแรงดันสูง (เช่น เครื่องกำเนิด Van de Graaf หรือเครื่องกำเนิด Wimshurst) มี EMF ขนาดใหญ่ที่วัดได้ในหน่วยล้านโวลต์ ในขณะที่ความต้านทานภายในวัดเป็นหลายร้อยเมกะโอห์ม ดังนั้นจึงไม่เหมาะสำหรับการได้รับ กระแสสูง.

ในทางตรงกันข้าม เซลล์กัลวานิก (เช่น แบตเตอรี่) มี EMF เท่ากับ 1 โวลต์ แม้ว่าความต้านทานภายในจะอยู่ในลำดับของเศษส่วนหรือมากสุด 10 โอห์ม ดังนั้นจึงสามารถรับกระแสของหน่วยและหลายสิบแอมแปร์ได้ จากเซลล์กัลวานิก

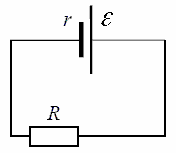
ไดอะแกรมนี้แสดงแหล่งที่มาจริงพร้อมโหลดที่เชื่อมต่อ พวกเขาถูกกำหนดที่นี่ แหล่งที่มาของ EMFความต้านทานภายในเช่นเดียวกับความต้านทานโหลด ตาม กฎของโอห์มสำหรับวงจรปิด, กระแสในวงจรนี้จะเท่ากับ:

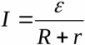
เนื่องจากส่วนวงจรภายนอกเป็นเนื้อเดียวกัน ดังนั้นจากกฎของโอห์มจึงสามารถพบแรงดันไฟฟ้าทั่วโหลดได้:

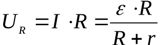
การแสดงความต้านทานของโหลดจากสมการแรกและแทนค่าลงในสมการที่สอง เราได้รับการพึ่งพาของแรงดันไฟฟ้าในโหลดของกระแสในวงจรปิด:

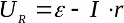
ในวงปิด EMF จะเท่ากับผลรวมของแรงดันตกที่องค์ประกอบวงจรภายนอกและความต้านทานภายในของแหล่งกำเนิด การพึ่งพาของแรงดันโหลดกับกระแสโหลดนั้นเป็นเชิงเส้นในอุดมคติ

กราฟแสดงสิ่งนี้ แต่ข้อมูลการทดลองสำหรับตัวต้านทานจริง (ตัดกันใกล้กับกราฟ) จะแตกต่างจากอุดมคติเสมอ:

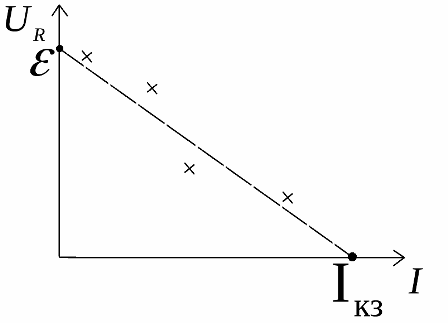
การทดลองและตรรกะแสดงว่าที่กระแสโหลดเป็นศูนย์ แรงดันวงจรภายนอกจะเท่ากับแรงเคลื่อนไฟฟ้าต้นทาง และที่แรงดันโหลดเป็นศูนย์ กระแสของวงจรจะเท่ากับ กระแสไฟฟ้าลัดวงจร… คุณสมบัติของวงจรจริงนี้ช่วยในการทดลองค้นหา EMF และความต้านทานภายในของแหล่งจริง

การทดลองตรวจหาความต้านทานภายใน

ในการพิจารณาลักษณะเหล่านี้ในการทดลองจะมีการสร้างกราฟของการพึ่งพาแรงดันไฟฟ้าในโหลดตามขนาดของกระแสไฟฟ้าหลังจากนั้นจะถูกประมาณค่าไปยังจุดตัดกับแกน

ที่จุดตัดของกราฟกับแกนแรงดันไฟฟ้าคือค่าของ emf แหล่งที่มาและที่จุดตัดกับแกนปัจจุบันคือค่าของกระแสลัดวงจร เป็นผลให้สูตรพบความต้านทานภายใน:

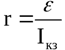
พลังงานที่เป็นประโยชน์ที่พัฒนาโดยแหล่งที่มาจะกระจายไปทั่วโหลด กราฟของการพึ่งพาพลังงานนี้กับความต้านทานโหลดจะแสดงในรูป เส้นโค้งนี้เริ่มต้นจากจุดตัดของแกนพิกัดที่จุดศูนย์ จากนั้นเพิ่มขึ้นเป็นค่ากำลังสูงสุด จากนั้นตกถึงศูนย์โดยมีค่าความต้านทานโหลดเท่ากับค่าอนันต์

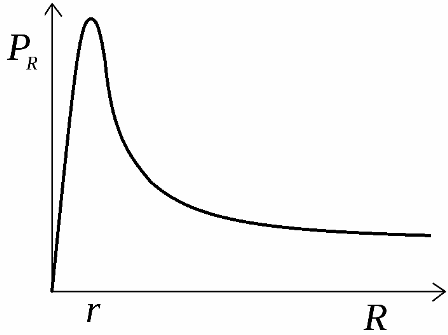
ในการหาค่าความต้านทานโหลดสูงสุดที่จะพัฒนากำลังไฟฟ้าสูงสุดตามทฤษฎีด้วยแหล่งที่กำหนด อนุพันธ์ของสูตรกำลังเทียบกับ R จะถูกนำมาใช้และตั้งค่าเป็นศูนย์ กำลังไฟฟ้าสูงสุดจะพัฒนาเมื่อความต้านทานของวงจรภายนอกเท่ากับความต้านทานของแหล่งจ่ายภายใน:

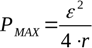
ข้อกำหนดนี้สำหรับกำลังสูงสุดที่ R = r ช่วยให้คุณสามารถทดลองหาค่าความต้านทานภายในของแหล่งจ่ายได้โดยการพล็อตกำลังไฟฟ้าที่ปล่อยที่โหลดเทียบกับค่าของความต้านทานโหลดการค้นหาความต้านทานโหลดที่เกิดขึ้นจริงมากกว่าตามทฤษฎีที่ให้พลังงานสูงสุดจะกำหนดความต้านทานภายในที่แท้จริงของแหล่งจ่ายไฟ

ประสิทธิภาพของแหล่งกระแสบ่งชี้อัตราส่วนของพลังงานสูงสุดที่กระจายไปยังโหลดต่อพลังงานทั้งหมดที่กำลังพัฒนา

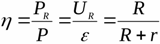
เป็นที่ชัดเจนว่าหากแหล่งที่มาพัฒนาพลังงานดังกล่าวจนได้รับพลังงานสูงสุดที่เป็นไปได้สำหรับแหล่งที่กำหนดที่โหลด ประสิทธิภาพของแหล่งที่มาจะเท่ากับ 50%