การทำงานของมอเตอร์แบบอะซิงโครนัส

การทำงานของมอเตอร์เหนี่ยวนำแสดงกราฟโดยขึ้นอยู่กับความเร็ว n2, ประสิทธิภาพ η, แรงบิดที่เป็นประโยชน์ (แรงบิดของเพลา) M2, ตัวประกอบกำลัง cos φ และกระแสสเตเตอร์ I1 บนกำลังไฟฟ้าที่มีประโยชน์ P2 ที่ U1 = const f1 = const

ลักษณะความเร็ว n2 = f (P2) ความเร็วโรเตอร์ของมอเตอร์เหนี่ยวนำ n2 = n1 (1 — s)

สไลด์ s = Pe2 / Rem เช่น การเลื่อนของมอเตอร์เหนี่ยวนำและความเร็วของมันถูกกำหนดโดยอัตราส่วนของการสูญเสียทางไฟฟ้าในโรเตอร์ต่อพลังงานแม่เหล็กไฟฟ้า ละเลยการสูญเสียทางไฟฟ้าในโรเตอร์ที่ไม่ได้ใช้งาน เราสามารถใช้ Pe2 = 0 ดังนั้น s ≈ 0 และ n20 ≈ n1

เมื่อภาระเพลาเพิ่มขึ้น เครื่องยนต์แบบอะซิงโครนัส อัตราส่วน s = Pe2 / Pem เพิ่มขึ้นถึงค่า 0.01 — 0.08 ที่โหลดเล็กน้อย ดังนั้นการพึ่งพา n2 = f (P2) จึงเป็นเส้นโค้งที่เอียงเล็กน้อยไปยังแกน abscissa อย่างไรก็ตาม เมื่อแรงต้านทานแอคทีฟของโรเตอร์มอเตอร์ r2 ' เพิ่มขึ้น ความชันของเส้นโค้งนี้จะเพิ่มขึ้น ในกรณีนี้ การเปลี่ยนแปลงความถี่ของมอเตอร์เหนี่ยวนำ n2 ที่มีความผันผวนของโหลด P2 จะเพิ่มขึ้นสิ่งนี้อธิบายได้จากความจริงที่ว่าเมื่อ r2 เพิ่มขึ้น การสูญเสียทางไฟฟ้าในโรเตอร์จะเพิ่มขึ้น

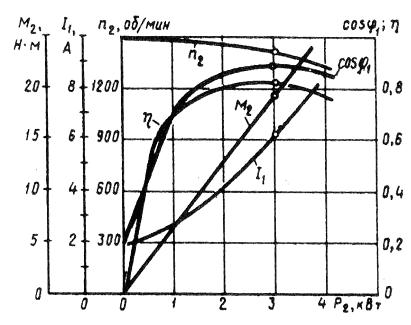
ข้าว. 1. ลักษณะการทำงานของมอเตอร์เหนี่ยวนำ

การพึ่งพา M2 = f (P2) การพึ่งพาแรงบิดที่มีประโยชน์จากเพลาของมอเตอร์แบบอะซิงโครนัส M2 บนกำลังที่มีประโยชน์ P2 นั้นถูกกำหนดโดยนิพจน์ M2 = P2 / ω2 = 60 P2 / (2πn2) = 9.55P2 / n2

โดยที่ P2 — พลังงานที่มีประโยชน์, W; ω2 = 2πf 2/60 คือความถี่เชิงมุมของการหมุนของโรเตอร์

จากนิพจน์นี้ว่าถ้า n2 = const กราฟ M2 = f2 (P2) จะเป็นเส้นตรง แต่ในมอเตอร์เหนี่ยวนำที่มีโหลด P2 เพิ่มขึ้น ความเร็วของโรเตอร์จะลดลง ดังนั้น โมเมนต์ที่มีประโยชน์ของเพลา M2 ที่มีโหลดเพิ่มขึ้นจะเพิ่มเร็วกว่าโหลดเล็กน้อย ดังนั้นกราฟ M2 = f (P2 ) มีรูปร่างเป็นเส้นโค้ง

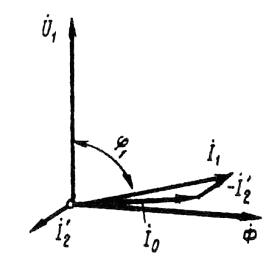ข้าว. 2. แผนภาพเวกเตอร์ของมอเตอร์เหนี่ยวนำที่โหลดต่ำ

การพึ่งพา cos φ1 = f (P2) เนื่องจากกระแสสเตเตอร์ของมอเตอร์เหนี่ยวนำ I1 มีองค์ประกอบปฏิกิริยา (อุปนัย) ที่จำเป็นในการสร้างสนามแม่เหล็กในสเตเตอร์ ตัวประกอบกำลังของมอเตอร์เหนี่ยวนำจึงน้อยกว่าความสามัคคี ค่าต่ำสุดของตัวประกอบกำลังสอดคล้องกับรอบเดินเบา สิ่งนี้อธิบายได้จากข้อเท็จจริงที่ว่ากระแสเดินเบาของมอเตอร์ไฟฟ้า I0 ที่โหลดใด ๆ ยังคงไม่เปลี่ยนแปลง ดังนั้น ที่โหลดมอเตอร์ต่ำ กระแสของสเตเตอร์จะมีน้อยและมีปฏิกิริยาเป็นส่วนใหญ่ (I1 ≈ I0) เป็นผลให้การเลื่อนเฟสของกระแสสเตเตอร์ที่เกี่ยวกับแรงดันไฟฟ้ามีความสำคัญ (φ1 ≈ φ0) น้อยกว่า 90 °เพียงเล็กน้อยเท่านั้น (รูปที่ 2)

ตัวประกอบกำลังไฟฟ้าที่ไม่มีโหลดของมอเตอร์เหนี่ยวนำมักจะน้อยกว่า 0.2เมื่อโหลดบนเพลามอเตอร์เพิ่มขึ้น ส่วนประกอบที่ใช้งานอยู่ของ I1 ปัจจุบันจะเพิ่มขึ้นและตัวประกอบกำลังจะเพิ่มขึ้นถึงค่าสูงสุด (0.80 — 0.90) ที่โหลดใกล้กับค่าที่ระบุ ภาระที่เพิ่มขึ้นบนเพลามอเตอร์นั้นมาพร้อมกับการลดลงของ cos φ1 ซึ่งอธิบายได้จากการเพิ่มขึ้นของความต้านทานเชิงอุปนัยของโรเตอร์ (x2s) เนื่องจากการเพิ่มขึ้นของสลิปและดังนั้นในความถี่ของ กระแสในโรเตอร์

เพื่อปรับปรุงตัวประกอบกำลังของมอเตอร์เหนี่ยวนำ สิ่งสำคัญอย่างยิ่งคือมอเตอร์ต้องทำงานเสมอ หรืออย่างน้อยก็เป็นช่วงที่มีนัยสำคัญ โดยมีโหลดใกล้เคียงกับโหลดที่กำหนด สิ่งนี้สามารถทำได้ด้วยการเลือกกำลังเครื่องยนต์ที่ถูกต้องเท่านั้น หากมอเตอร์ทำงานภายใต้โหลดเป็นระยะเวลาหนึ่ง ดังนั้นเพื่อเพิ่ม cos φ1 ขอแนะนำให้ลดแรงดันไฟฟ้า U1 ที่จ่ายให้กับมอเตอร์ ตัวอย่างเช่น ในมอเตอร์ที่ทำงานเมื่อขดลวดสเตเตอร์เชื่อมต่อกับเดลต้า สามารถทำได้โดยการต่อขดลวดสเตเตอร์อีกครั้งในดาว ซึ่งจะทำให้แรงดันเฟสลดลงตามปัจจัย ในกรณีนี้ ฟลักซ์แม่เหล็กของสเตเตอร์และด้วยเหตุนี้กระแสแม่เหล็กจึงลดลงประมาณหนึ่งปัจจัย นอกจากนี้ส่วนประกอบที่ใช้งานของกระแสสเตเตอร์จะเพิ่มขึ้นเล็กน้อย ทั้งหมดนี้มีส่วนช่วยในการเพิ่มตัวประกอบกำลังของเครื่องยนต์

ในรูป 3 แสดงกราฟของการพึ่งพาของ cos φ1, มอเตอร์แบบอะซิงโครนัสบนโหลด, เมื่อขดลวดสเตเตอร์เชื่อมต่อในรูปดาว (เส้นโค้ง 1) และเดลต้า (เส้นโค้ง 2)

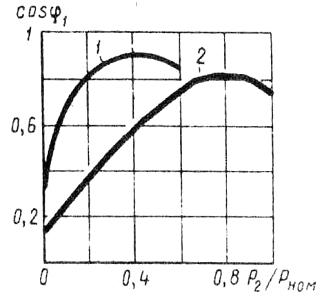
ข้าว. 3. การพึ่งพา cos φ1กับโหลดเมื่อเชื่อมต่อขดลวดสเตเตอร์ของมอเตอร์กับดาว (1) และเดลต้า (2)