กระแสอิมพัลส์

ในอุปกรณ์อิเล็กทรอนิกส์ต่างๆ เช่น ในอุปกรณ์อิเล็กทรอนิกส์และเซมิคอนดักเตอร์ เช่น ในเครื่องขยายเสียง วงจรเรียงกระแส วิทยุ เครื่องกำเนิดไฟฟ้า โทรทัศน์ ตลอดจนในไมโครโฟนคาร์บอน โทรเลข และอุปกรณ์อื่นๆ อีกมากมาย มีการใช้กระแสกระเพื่อมและแรงดันไฟฟ้ากันอย่างแพร่หลาย... ตามลำดับ เพื่อไม่ให้ใช้เหตุผลซ้ำสองครั้งเราจะพูดถึงกระแสเท่านั้น แต่ทุกสิ่งที่เกี่ยวข้องกับกระแสก็เป็นจริงสำหรับแรงดันไฟฟ้าเช่นกัน

กระแสพัลส์ที่มีทิศทางคงที่แต่เปลี่ยนค่าได้แตกต่างกัน บางครั้งค่าปัจจุบันเปลี่ยนจากค่าสูงสุดเป็นค่าต่ำสุดที่ไม่ใช่ศูนย์ ในกรณีอื่น ๆ กระแสจะลดลงเป็นศูนย์ ถ้า วงจรไฟฟ้ากระแสตรง ถูกขัดจังหวะที่ความถี่หนึ่ง จากนั้นบางช่วงเวลาจะไม่มีกระแสไฟฟ้าในวงจร

ในรูป 1 แสดงกราฟของกระแสคลื่นต่างๆ ในรูป 1, a, b, การเปลี่ยนแปลงของกระแสเกิดขึ้นตาม เส้นโค้งไซน์, แต่ไม่ควรพิจารณากระแสเหล่านี้ว่าเป็นกระแสสลับไซน์เนื่องจากทิศทาง (เครื่องหมาย) ของกระแสไม่เปลี่ยนแปลง ในรูป1, c แสดงกระแสที่ประกอบด้วยพัลส์ที่แยกจากกัน นั่นคือ "การกระแทก" ของกระแสไฟฟ้าที่มีอายุสั้น แยกออกจากกันโดยการหยุดชั่วคราวในระยะเวลาที่มากขึ้นหรือน้อยลง และมักเรียกว่ากระแสพัลซิ่ง กระแสพัลส์ที่แตกต่างกันนั้นแตกต่างกันในรูปร่างและระยะเวลาของพัลส์รวมถึงอัตราการเกิดซ้ำ

เป็นการสะดวกที่จะพิจารณากระแสที่เต้นเป็นจังหวะชนิดใดก็ได้เป็นผลรวมของกระแสสองกระแส — ทางตรงและกระแสสลับ เรียกว่า กระแสเทอมหรือกระแสคอมโพเนนต์ กระแสที่เต้นเป็นจังหวะมีส่วนประกอบของ DC และ AC เรื่องนี้ดูแปลกสำหรับหลาย ๆ คน อันที่จริงแล้ว กระแสที่เต้นเป็นจังหวะคือกระแสที่ไหลตลอดเวลาในทิศทางเดียวและเปลี่ยนค่าของมัน

คุณจะบอกได้อย่างไรว่ามีไฟฟ้ากระแสสลับที่เปลี่ยนทิศทาง? อย่างไรก็ตาม หากกระแสสองกระแส - ทางตรงและกระแสสลับ - ผ่านเส้นลวดเดียวกันพร้อมกัน ปรากฎว่ากระแสที่เต้นเป็นจังหวะจะไหลในเส้นนั้น (รูปที่ 2) ในกรณีนี้ แอมพลิจูดของกระแสสลับไม่ควรเกินค่าของกระแสตรง กระแสตรงและกระแสสลับไม่สามารถไหลผ่านสายไฟแยกกันได้ พวกเขาเพิ่มการไหลของอิเล็กตรอนทั่วไปที่มีคุณสมบัติทั้งหมดของกระแสที่เต้นเป็นจังหวะ

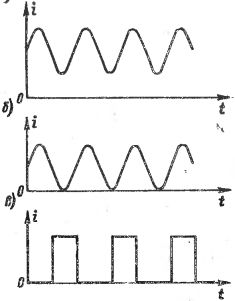
ข้าว. 1. กราฟของกระแสคลื่นต่างๆ

การเพิ่มกระแส AC และ DC สามารถแสดงแบบกราฟิกได้ ในรูป 2 แสดงกราฟของกระแสตรงเท่ากับ 15 mA และกระแสสลับที่มีแอมพลิจูด 10 mA หากเรารวมค่าของกระแสเหล่านี้สำหรับแต่ละจุดในเวลา โดยคำนึงถึงทิศทาง (สัญญาณ) ของกระแส เราจะได้กราฟกระแสคลื่นที่แสดงในรูปที่ 2 ด้วยเส้นหนา กระแสนี้แตกต่างกันไปตั้งแต่ต่ำ 5 mA ถึงสูง 25 mA

การเพิ่มกระแสที่พิจารณาแล้วเป็นการยืนยันความถูกต้องของการแสดงกระแสที่เต้นเป็นจังหวะเป็นผลรวมของกระแสตรงและกระแสสลับ ความถูกต้องของการแสดงนี้ได้รับการยืนยันด้วยความจริงที่ว่าด้วยความช่วยเหลือของอุปกรณ์บางอย่างสามารถแยกส่วนประกอบของกระแสนี้ออกจากกันได้

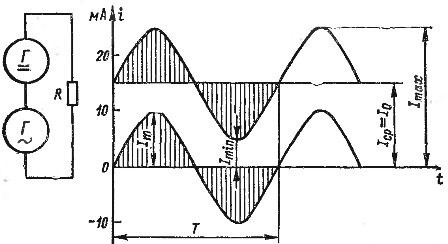
ข้าว. 2. รับกระแสเป็นจังหวะโดยการเพิ่มกระแสตรงและกระแสสลับ

ควรเน้นว่ากระแสใด ๆ สามารถแสดงเป็นผลรวมของกระแสต่าง ๆ ได้เสมอ ตัวอย่างเช่น กระแส 5 A สามารถพิจารณาผลรวมของกระแส 2 และ 3 A ที่ไหลในทิศทางเดียว หรือผลรวมของกระแส 8 และ 3 A ที่ไหลในทิศทางต่างๆ กล่าวคือ ความแตกต่างระหว่างกระแส 8 และ 3 A. ไม่ใช่เรื่องยากที่จะหาชุดค่าผสมอื่น ๆ ของกระแสตั้งแต่สองกระแสขึ้นไปที่ให้ผลรวมเป็น 5 A.

ที่นี่มีความคล้ายคลึงกันอย่างสมบูรณ์กับหลักการของการบวกและการสลายตัวของแรง หากแรงสองแรงที่มีทิศทางเท่ากันกระทำต่อวัตถุใด ๆ แรงเหล่านั้นจะถูกแทนที่ด้วยแรงร่วมหนึ่งแรง แรงที่กระทำในทิศทางตรงกันข้ามสามารถถูกแทนที่ด้วยความแตกต่างของหน่วย ในทางกลับกัน แรงที่กำหนดสามารถถือเป็นผลรวมของแรงที่กำกับเท่ากันหรือผลต่างระหว่างแรงที่กำกับตรงข้ามกัน

ไม่จำเป็นต้องแยกกระแสสลับโดยตรงหรือไซน์ให้เป็นกระแสคอมโพเนนต์ หากเราแทนที่กระแสที่เต้นเป็นจังหวะด้วยผลรวมของกระแสตรงและกระแสสลับ จากนั้นใช้กฎที่ทราบของกระแสตรงและกระแสสลับกับกระแสองค์ประกอบเหล่านี้ เป็นไปได้ที่จะแก้ปัญหามากมายและทำการคำนวณที่จำเป็นเกี่ยวกับกระแสที่เต้นเป็นจังหวะ

แนวคิดของกระแสพัลซิ่งเป็นผลรวมของกระแสตรงและกระแสสลับเป็นเรื่องปกติแน่นอนว่าไม่สามารถสันนิษฐานได้ว่าในช่วงเวลาหนึ่งกระแสตรงและกระแสสลับจะไหลเข้าหากันตามเส้นลวด ในความเป็นจริงไม่มีกระแสอิเล็กตรอนสองกระแสที่ตรงกันข้าม

ในความเป็นจริง กระแสที่เต้นเป็นจังหวะเป็นกระแสเดียวที่เปลี่ยนค่าเมื่อเวลาผ่านไป ถูกต้องกว่าที่จะบอกว่าแรงดันพัลซิ่งหรือ EMF ที่เต้นเป็นจังหวะสามารถแสดงเป็นผลรวมของส่วนประกอบคงที่และตัวแปร

ตัวอย่างเช่น ในรูปที่ 2 แสดงให้เห็นว่าค่าคงที่ emf ของตัวสร้างหนึ่งถูกเพิ่มเข้าไปในตัวแปร emf ของตัวสร้างอีกตัวในทางพีชคณิต เป็นผลให้เรามี EMF ที่เต้นเป็นจังหวะซึ่งทำให้เกิดกระแสที่เต้นเป็นจังหวะที่สอดคล้องกัน อย่างไรก็ตามตามเงื่อนไขแล้วสามารถพิจารณาได้ว่า EMF คงที่สร้างกระแสตรงในวงจรและ EMF สลับ - กระแสสลับซึ่งเมื่อรวมกันแล้วจะสร้างกระแสเป็นจังหวะ

แต่ละกระแสที่เต้นเป็นจังหวะสามารถระบุได้ด้วยค่าสูงสุดและต่ำสุดของ Itax และ Itin รวมถึงส่วนประกอบคงที่และตัวแปร ส่วนประกอบคงที่แสดงด้วย I0 หากส่วนประกอบกระแสสลับเป็นกระแสไซน์ แอมพลิจูดของมันจะแสดงด้วยมัน (ปริมาณทั้งหมดนี้แสดงในรูปที่ 2)

ไม่ควรสับสนกับ It และ Itax นอกจากนี้ ค่าสูงสุดของ Imax คลื่นปัจจุบันไม่ควรเรียกว่าแอมพลิจูด คำว่าแอมพลิจูดมักหมายถึงกระแสสลับเท่านั้น เกี่ยวกับกระแสที่เต้นเป็นจังหวะเราสามารถพูดถึงความกว้างขององค์ประกอบที่แปรผันได้เท่านั้น

ส่วนประกอบคงที่ของกระแสที่เต้นเป็นจังหวะสามารถเรียกว่าค่าเฉลี่ย Iav นั่นคือค่าเฉลี่ยเลขคณิต แท้จริงแล้ว หากเราพิจารณาการเปลี่ยนแปลงในช่วงเวลาหนึ่งของการเต้นของกระแสที่แสดงในรูป2 จะเห็นสิ่งต่อไปนี้อย่างชัดเจน: ในครึ่งแรกจะมีการเพิ่มค่าจำนวนหนึ่งให้กับกระแส 15 mA โดยเปลี่ยนส่วนประกอบปัจจุบันซึ่งแตกต่างจาก 0 ถึง 10 mA และกลับเป็น 0 และในช่วงครึ่งหลัง - รอบค่าปัจจุบันเดียวกันจะถูกลบออกจาก 15 mA ปัจจุบัน

ดังนั้นกระแส 15 mA จึงเป็นค่าเฉลี่ยจริงๆ เนื่องจากกระแสคือการถ่ายโอนประจุไฟฟ้าผ่านส่วนตัดขวางของเส้นลวด ดังนั้น Iav จึงเป็นค่าของไฟฟ้ากระแสตรงที่ในหนึ่งช่วงเวลา (หรือสำหรับจำนวนคาบทั้งหมด) มีปริมาณไฟฟ้าเท่ากันกับกระแสที่เต้นเป็นจังหวะนี้ .

สำหรับไฟฟ้ากระแสสลับไซน์ ค่า Iav ต่อคาบเป็นศูนย์ เนื่องจากปริมาณไฟฟ้าที่ผ่านหน้าตัดของตัวนำในครึ่งเวลาหนึ่งเท่ากับปริมาณไฟฟ้าที่ผ่านในทิศทางตรงกันข้ามในอีกครึ่งคาบ บนกราฟของกระแสที่แสดงการพึ่งพาของกระแส i ตามเวลา t ปริมาณไฟฟ้าที่กระแสไฟฟ้าถูกแสดงโดยพื้นที่ของตัวเลขที่ล้อมรอบด้วยเส้นโค้งปัจจุบัน เนื่องจากปริมาณไฟฟ้าถูกกำหนดโดย สินค้าที่มัน.

สำหรับกระแสคลื่นไซน์ พื้นที่ของครึ่งคลื่นบวกและลบจะเท่ากัน ในกระแสพัลซิ่งที่แสดงในรูปที่ 2 ในช่วงครึ่งแรก ปริมาณไฟฟ้าที่ดำเนินการโดยส่วนประกอบ AC จะถูกเพิ่มเข้ากับปริมาณไฟฟ้าที่ดำเนินการโดย Iav ปัจจุบัน (พื้นที่แรเงาในรูป) และในช่วงครึ่งหลังจะมีการถอนไฟฟ้าในปริมาณที่เท่ากัน เป็นผลให้มีการถ่ายโอนไฟฟ้าในปริมาณที่เท่ากันตลอดทั้งช่วงเวลาเช่นเดียวกับ Iav กระแสตรงเดียวนั่นคือพื้นที่ของสี่เหลี่ยมผืนผ้า Iav T เท่ากับพื้นที่ที่ล้อมรอบด้วยเส้นโค้งกระแสคลื่น

ดังนั้นส่วนประกอบคงที่หรือค่าเฉลี่ยของกระแสไฟฟ้าจะถูกกำหนดโดยการถ่ายโอนประจุไฟฟ้าผ่านส่วนตัดขวางของเส้นลวด

สมการปัจจุบันแสดงในรูปที่ 2 ควรเขียนในรูปแบบต่อไปนี้อย่างชัดเจน:

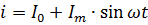
ต้องคำนวณกำลังของกระแสที่เต้นเป็นจังหวะเป็นผลรวมของกำลังของกระแสส่วนประกอบ เช่น ถ้ากระแสดังรูป 2 ผ่านตัวต้านทานของความต้านทาน R แล้วพลังของมันคือ

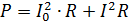
โดยที่ I = 0.7Im คือค่า rms ของส่วนประกอบตัวแปร

คุณสามารถแนะนำแนวคิดของค่า rms ของรหัสปัจจุบันของคลื่น กำลังคำนวณตามปกติ:

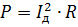
สมการนิพจน์นี้กับนิพจน์ก่อนหน้าและลดด้วย R เราได้รับ:

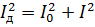
สามารถรับความสัมพันธ์เดียวกันได้สำหรับความเครียด