กฎของแอมแปร์

ในบทความนี้ เราจะพูดถึงกฎของแอมแปร์ ซึ่งเป็นหนึ่งในกฎพื้นฐานของอิเล็กโทรไดนามิกส์ แรงของแอมแปร์กำลังทำงานอยู่ในปัจจุบันในเครื่องจักรไฟฟ้าและการติดตั้งจำนวนมาก และด้วยแรงของแอมแปร์ในศตวรรษที่ 20 ความก้าวหน้าที่เกี่ยวข้องกับการใช้พลังงานไฟฟ้าในหลายๆ ด้านของการผลิตจึงเป็นไปได้ กฎของแอมแปร์ยังคงยืนหยัดมาจนถึงทุกวันนี้และยังคงรับใช้วิศวกรรมสมัยใหม่อย่างซื่อสัตย์ ดังนั้นอย่าลืมว่าเราเป็นหนี้ใครบ้างและเริ่มต้นอย่างไร

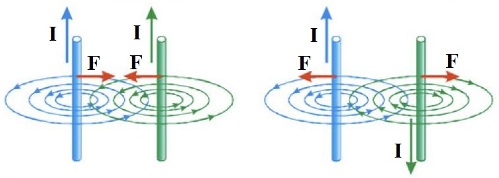
ในปี 1820 Andre Marie Ampere นักฟิสิกส์ชาวฝรั่งเศสผู้ยิ่งใหญ่ได้ประกาศการค้นพบของเขา เขาพูดที่ Academy of Sciences เกี่ยวกับปรากฏการณ์ของปฏิสัมพันธ์ของตัวนำสองตัวที่มีกระแส: ตัวนำที่มีกระแสตรงข้ามกันจะผลักกันและด้วยกระแสตรงพวกมันจะดึงดูดซึ่งกันและกัน แอมแปร์ยังเสนอว่าแม่เหล็กเป็นไฟฟ้าทั้งหมด

ในบางครั้งนักวิทยาศาสตร์ได้ทำการทดลองและในที่สุดก็ยืนยันข้อสันนิษฐานของเขา ในที่สุด ในปี พ.ศ. 2369 เขาได้เผยแพร่ทฤษฎีปรากฏการณ์อิเล็กโทรไดนามิกที่ได้รับมาจากประสบการณ์โดยเฉพาะจากจุดนั้น ความคิดเกี่ยวกับของไหลแม่เหล็กก็ถูกไล่ออกโดยไม่จำเป็น เนื่องจากแม่เหล็กนั้นเกิดจากกระแสไฟฟ้า

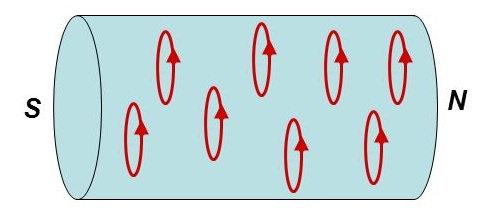
แอมแปร์สรุปได้ว่าแม่เหล็กถาวรยังมีกระแสไฟฟ้าอยู่ภายใน กระแสโมเลกุลและอะตอมแบบวงกลมตั้งฉากกับแกนที่ผ่านขั้วของแม่เหล็กถาวร ขดลวดทำตัวเหมือนแม่เหล็กถาวรที่กระแสไหลเป็นเกลียว แอมแปร์ได้รับสิทธิ์อย่างเต็มที่ในการยืนยันอย่างมั่นใจว่า: "ปรากฏการณ์ทางแม่เหล็กทั้งหมดจะลดลงเป็นการกระทำทางไฟฟ้า"

ในงานวิจัยของเขา แอมแปร์ยังได้ค้นพบความสัมพันธ์ระหว่างแรงปฏิสัมพันธ์ของธาตุปัจจุบันกับขนาดของกระแสเหล่านี้ นอกจากนี้เขายังพบการแสดงออกของแรงนี้ด้วย แอมแปร์ชี้ให้เห็นว่าแรงปฏิสัมพันธ์ของกระแสน้ำไม่ได้เป็นศูนย์กลางเหมือนแรงโน้มถ่วง สูตรที่ได้รับแอมแปร์รวมอยู่ในตำราเกี่ยวกับอิเล็กโทรไดนามิกส์ทุกเล่มในปัจจุบัน

แอมแปร์พบว่ากระแสจากทิศทางตรงกันข้ามจะผลักกันและกระแสจากทิศทางเดียวกันจะดึงดูดกัน หากกระแสตั้งฉากกัน ก็จะไม่มีอันตรกิริยาทางแม่เหล็กระหว่างกัน นี่เป็นผลจากการตรวจสอบของนักวิทยาศาสตร์เกี่ยวกับการโต้ตอบของกระแสไฟฟ้าซึ่งเป็นสาเหตุที่แท้จริงของการโต้ตอบของแม่เหล็ก แอมแปร์ค้นพบกฎของการโต้ตอบทางกลของกระแสไฟฟ้าและแก้ปัญหาของปฏิสัมพันธ์ทางแม่เหล็กได้

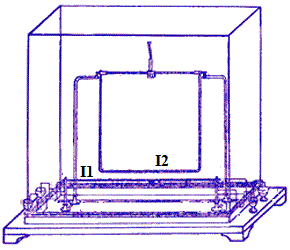
เพื่อชี้แจงกฎที่แรงปฏิสัมพันธ์เชิงกลของกระแสเกี่ยวข้องกับปริมาณอื่น ๆ เป็นไปได้ที่จะทำการทดลองที่คล้ายกับการทดลองของแอมแปร์ในปัจจุบันในการทำเช่นนี้สายที่ค่อนข้างยาวที่มี I1 ปัจจุบันจะคงที่และสายสั้นที่มี I2 ปัจจุบันจะถูกทำให้เคลื่อนที่ได้ ตัวอย่างเช่น ด้านล่างของเฟรมที่เคลื่อนที่ได้พร้อมกับกระแสจะเป็นสายที่สอง เฟรมเชื่อมต่อกับไดนาโมมิเตอร์เพื่อวัดแรง F ที่กระทำกับเฟรมเมื่อตัวนำไฟฟ้าขนานกัน

ในขั้นต้น ระบบมีความสมดุลและระยะห่าง R ระหว่างสายของการตั้งค่าการทดลองนั้นน้อยกว่ามากเมื่อเทียบกับความยาว l ของสายเหล่านี้ จุดประสงค์ของการทดลองคือเพื่อวัดแรงผลักของสายไฟ

กระแสในสายไฟทั้งแบบอยู่กับที่และแบบเคลื่อนที่สามารถควบคุมได้โดยใช้รีโอสแตท โดยการเปลี่ยนระยะทาง R ระหว่างสาย โดยการเปลี่ยนกระแสในแต่ละสาย เราสามารถค้นหาการพึ่งพาได้อย่างง่ายดาย ดูว่าความแข็งแรงของการโต้ตอบเชิงกลของสายไฟนั้นขึ้นอยู่กับกระแสและระยะทางอย่างไร

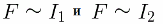
หาก I2 ปัจจุบันในเฟรมเคลื่อนที่ไม่เปลี่ยนแปลง และ I1 ปัจจุบันในเส้นลวดเคลื่อนที่เพิ่มขึ้นตามจำนวนครั้งที่กำหนด แรง F ของการโต้ตอบของเส้นลวดจะเพิ่มขึ้นในจำนวนที่เท่ากัน ในทำนองเดียวกัน สถานการณ์จะเกิดขึ้นหาก I1 ปัจจุบันในเส้นลวดคงที่ไม่มีการเปลี่ยนแปลงและ I2 ปัจจุบันในเฟรมเปลี่ยนไป จากนั้นแรงโต้ตอบ F จะเปลี่ยนไปในลักษณะเดียวกับเมื่อ I1 ปัจจุบันเปลี่ยนในเส้นลวดอยู่กับที่โดยมี I2 กระแสคงที่ใน กรอบ. ดังนั้นเราจึงได้ข้อสรุปที่ชัดเจน - แรงปฏิสัมพันธ์ของสาย F เป็นสัดส่วนโดยตรงกับ I1 ปัจจุบันและ I2 ปัจจุบัน

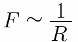
หากตอนนี้เราเปลี่ยนระยะทาง R ระหว่างสายที่มีปฏิสัมพันธ์ ปรากฎว่าเมื่อระยะทางนี้เพิ่มขึ้น แรง F จะลดลงและลดลงตามปัจจัยเดียวกับระยะทาง Rดังนั้นแรงของการโต้ตอบทางกล F ของสายไฟที่มีกระแส I1 และ I2 จะแปรผกผันกับระยะทาง R ระหว่างพวกมัน

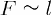
ด้วยการปรับขนาด l ของเส้นลวดที่เคลื่อนที่ได้ จึงเป็นเรื่องง่ายที่จะตรวจสอบให้แน่ใจว่าแรงนั้นเป็นสัดส่วนโดยตรงกับความยาวของด้านที่กระทบกัน

ด้วยเหตุนี้ คุณสามารถป้อนปัจจัยสัดส่วนและเขียน:

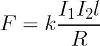
สูตรนี้ช่วยให้คุณหาแรง F ซึ่งสนามแม่เหล็กที่สร้างขึ้นโดยตัวนำที่มีความยาวไม่สิ้นสุดที่มีกระแส I1 กระทำกับส่วนขนานของตัวนำที่มีกระแสไฟฟ้า I2 ในขณะที่ความยาวของส่วนคือ l และ R คือระยะทาง ระหว่างตัวนำที่มีปฏิสัมพันธ์ สูตรนี้มีความสำคัญอย่างยิ่งในการศึกษาแม่เหล็ก

อัตราส่วนภาพสามารถแสดงในรูปของค่าคงที่แม่เหล็กได้ดังนี้:

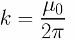
จากนั้นสูตรจะอยู่ในรูปแบบ:

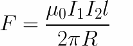
แรง F ปัจจุบันเรียกว่าแรงของแอมแปร์ และกฎที่กำหนดขนาดของแรงนี้คือกฎของแอมแปร์ กฎของแอมแปร์เรียกอีกอย่างว่ากฎที่กำหนดแรงที่สนามแม่เหล็กกระทำต่อส่วนเล็ก ๆ ของตัวนำที่มีกระแสไฟฟ้า:

«แรง dF ที่สนามแม่เหล็กกระทำต่อองค์ประกอบ dl ของตัวนำที่มีกระแสในสนามแม่เหล็กเป็นสัดส่วนโดยตรงกับความแรงของ dI ปัจจุบันในตัวนำและผลคูณเวกเตอร์ขององค์ประกอบที่มีความยาว dl ของ ตัวนำและการเหนี่ยวนำแม่เหล็ก B «:

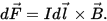
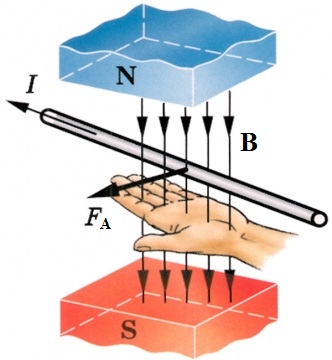
ทิศทางของแรงแอมแปร์ถูกกำหนดโดยกฎการคำนวณผลคูณของเวกเตอร์ ซึ่งสะดวกต่อการจำโดยใช้กฎมือซ้าย ซึ่งหมายถึง กฎหมายพื้นฐานของวิศวกรรมไฟฟ้าและโมดูลัสแรงแอมแปร์สามารถคำนวณได้จากสูตร:

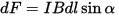
ในที่นี้ อัลฟาคือมุมระหว่างเวกเตอร์การเหนี่ยวนำแม่เหล็กกับทิศทางปัจจุบัน

เห็นได้ชัดว่า แรงแอมแปร์จะสูงสุดเมื่อองค์ประกอบของตัวนำที่มีกระแสไฟฟ้าตั้งฉากกับเส้นของการเหนี่ยวนำแม่เหล็ก B

ด้วยพลังของแอมแปร์ เครื่องใช้ไฟฟ้าจำนวนมากจึงทำงานในปัจจุบัน โดยสายไฟที่มีกระแสไฟฟ้ากระทบกันและกับสนามแม่เหล็กไฟฟ้า เครื่องกำเนิดไฟฟ้าและมอเตอร์ส่วนใหญ่ไม่ทางใดก็ทางหนึ่งใช้พลังงานแอมแปร์ในการทำงาน โรเตอร์ของมอเตอร์ไฟฟ้าหมุนในสนามแม่เหล็กของสเตเตอร์เนื่องจากแรงของแอมแปร์

ยานพาหนะไฟฟ้า: รถราง รถไฟฟ้า รถยนต์ไฟฟ้า — ล้วนใช้กำลังของแอมแปร์เพื่อทำให้ล้อหมุนในที่สุด ล็อคไฟฟ้า, ประตูลิฟต์, ฯลฯ ลำโพง, ลำโพง - สนามแม่เหล็กของขดลวดปัจจุบันมีปฏิสัมพันธ์กับสนามแม่เหล็กของแม่เหล็กถาวร, ก่อตัวเป็นคลื่นเสียง ในที่สุด พลาสมาจะถูกบีบอัดในโทคามักเนื่องจากแรงของแอมแปร์