วิธีการคำนวณค่าความเหนี่ยวนำ
เช่นเดียวกับวัตถุที่มีมวลในกลศาสตร์ต่อต้านความเร่งในอวกาศ แสดงความเฉื่อย ดังนั้นการเหนี่ยวนำจะป้องกันไม่ให้กระแสในตัวนำเปลี่ยนแปลง และแสดง EMF ที่เหนี่ยวนำตัวเอง นี่คือ EMF ของการเหนี่ยวนำตัวเอง ซึ่งต่อต้านทั้งกระแสที่ลดลง พยายามรักษาไว้ และกระแสที่เพิ่มขึ้น พยายามลดกระแส
ความจริงก็คือในกระบวนการเปลี่ยน (เพิ่มหรือลด) กระแสในวงจร ฟลักซ์แม่เหล็กที่สร้างขึ้นโดยกระแสนี้ก็เปลี่ยนไปเช่นกัน ซึ่งส่วนใหญ่จะอยู่ในพื้นที่จำกัดโดยวงจรนี้ และเมื่อฟลักซ์แม่เหล็กเพิ่มขึ้นหรือลดลง มันจะเหนี่ยวนำ EMF ของการเหนี่ยวนำตัวเอง (ตามกฎของ Lenz — เทียบกับสาเหตุที่ทำให้เกิด นั่นคือ เทียบกับกระแสที่กล่าวถึงในตอนต้น) ทั้งหมดในวงจรเดียวกัน ความเหนี่ยวนำ L ที่นี่เรียกว่าปัจจัยสัดส่วนระหว่างกระแส I และฟลักซ์แม่เหล็กทั้งหมด Φ กระแสนี้สร้างขึ้นโดย:
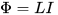
ดังนั้นยิ่งค่าความเหนี่ยวนำของวงจรสูงเท่าไร วงจรก็จะยิ่งแรงกว่าสนามแม่เหล็กที่เกิดขึ้นเท่านั้น จึงป้องกันกระแสไม่ให้เปลี่ยนแปลง (เป็นสนามที่สร้างวงจรขึ้นมา) ดังนั้น กระแสจึงใช้เวลานานขึ้นในการเปลี่ยนผ่านค่าความเหนี่ยวนำที่มากขึ้น ด้วยแรงดันไฟที่เท่ากัน ข้อความต่อไปนี้ยังเป็นความจริง: ยิ่งค่าความเหนี่ยวนำสูงเท่าใด แรงดันไฟฟ้าคร่อมวงจรก็จะยิ่งมากขึ้นเมื่อฟลักซ์แม่เหล็กไหลผ่านวงจรนั้นเปลี่ยนไป

สมมติว่าเราเปลี่ยนฟลักซ์แม่เหล็กในบางพื้นที่ด้วยอัตราคงที่ จากนั้นให้ครอบคลุมบริเวณนี้ด้วยวงจรต่างๆ เราจะได้แรงดันไฟฟ้าเพิ่มขึ้นบนวงจรที่มีค่าความเหนี่ยวนำมากกว่า (หม้อแปลง ขดลวด Rumkorf ฯลฯ ใช้หลักการนี้)
แต่ตัวเหนี่ยวนำลูปคำนวณอย่างไร จะหาปัจจัยสัดส่วนระหว่างกระแสและฟลักซ์แม่เหล็กได้อย่างไร? สิ่งแรกที่ต้องจำไว้คือการเปลี่ยนแปลงความเหนี่ยวนำในเฮนรี่ (H) ที่ขั้วของวงจรที่มีความเหนี่ยวนำ 1 เฮนรี่ ถ้ากระแสในวงจรเปลี่ยนไป 1 แอมแปร์ต่อวินาที แรงดัน 1 โวลต์จะปรากฏขึ้น
ขนาดของความเหนี่ยวนำขึ้นอยู่กับพารามิเตอร์สองตัว: ขนาดทางเรขาคณิตของวงจร (ความยาว ความกว้าง จำนวนรอบ ฯลฯ) และคุณสมบัติทางแม่เหล็กของตัวกลาง (เช่น หากมีแกนเฟอร์ไรต์อยู่ภายใน ค่าความเหนี่ยวนำจะมากกว่าถ้าไม่มีแกนอยู่ภายใน)
ในการคำนวณค่าความเหนี่ยวนำที่เกิดขึ้น จำเป็นต้องรู้ว่าขดลวดจะมีรูปร่างอย่างไร และสื่อแม่เหล็กจะซึมผ่านได้อย่างไร (การซึมผ่านของแม่เหล็กสัมพัทธ์ของตัวกลางเป็นปัจจัยสัดส่วนระหว่างการซึมผ่านของแม่เหล็กของสุญญากาศและแม่เหล็ก การซึมผ่านของตัวกลางที่กำหนดแน่นอนว่ามันแตกต่างกันตามวัสดุที่แตกต่างกัน) …
ลองดูสูตรสำหรับคำนวณความเหนี่ยวนำของขดลวดรูปแบบที่พบมากที่สุด (โซลินอยด์ทรงกระบอก, วงแหวนและลวดยาว)
นี่คือสูตรในการคำนวณความเหนี่ยวนำ โซลินอยด์ — ขดลวดซึ่งมีความยาวมากกว่าเส้นผ่านศูนย์กลางมาก:
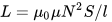
อย่างที่คุณเห็นเมื่อทราบจำนวนรอบ N ความยาวของขดลวด l และพื้นที่หน้าตัดของขดลวด S เราจะพบค่าความเหนี่ยวนำโดยประมาณของขดลวดโดยไม่มีแกนหรือมีแกนในขณะที่แม่เหล็ก ความสามารถในการซึมผ่านของสุญญากาศเป็นค่าคงที่:
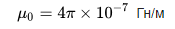
ความเหนี่ยวนำของขดลวด Toroidal โดยที่ h คือความสูงของ Toroid, r คือเส้นผ่านศูนย์กลางภายในของ Toroid, R คือเส้นผ่านศูนย์กลางภายนอกของ Toroid:
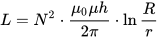
ความเหนี่ยวนำของเส้นลวดบาง ๆ (รัศมีของหน้าตัดเล็กกว่าความยาวมาก) โดยที่ l คือความยาวของเส้นลวด และ r คือรัศมีของหน้าตัด Mu ที่มีดัชนี i และ e คือ การซึมผ่านของแม่เหล็กสัมพัทธ์ของสภาพแวดล้อมภายใน (ภายใน, วัสดุตัวนำ) และสภาพแวดล้อมภายนอก (ภายนอก, วัสดุภายนอกตัวนำ):
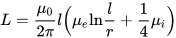
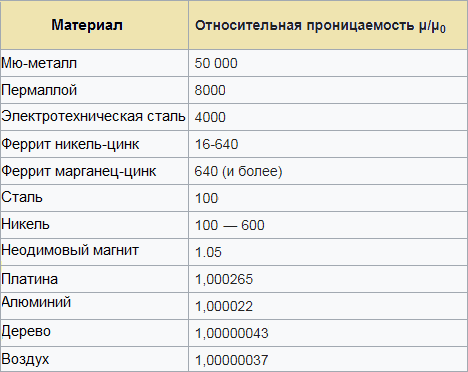
ตารางการอนุญาตสัมพัทธ์จะช่วยให้คุณประเมินค่าความเหนี่ยวนำที่คุณคาดหวังได้จากวงจร (ลวด, ขดลวด) โดยใช้วัสดุแม่เหล็กบางอย่างเป็นแกน: