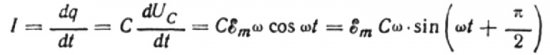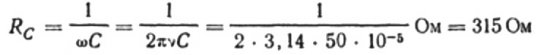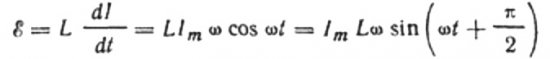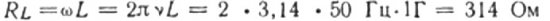ความต้านทานตัวเก็บประจุและอุปนัยในวงจรไฟฟ้ากระแสสลับ
หากเรารวมตัวเก็บประจุไว้ในวงจรไฟฟ้ากระแสตรง เราพบว่ามันมีความต้านทานไม่สิ้นสุดเพราะกระแสตรงไม่สามารถผ่านไดอิเล็กตริกระหว่างแผ่นได้ เนื่องจากไดอิเล็กตริกตามคำนิยามไม่ได้นำกระแสไฟฟ้าตรง
ตัวเก็บประจุทำลายวงจรไฟฟ้ากระแสตรง แต่ถ้าตอนนี้ตัวเก็บประจุตัวเดียวกันรวมอยู่ในวงจรไฟฟ้ากระแสสลับแล้ว ปรากฎว่าตัวเก็บประจุของมันดูเหมือนจะไม่แตกหักอย่างสมบูรณ์ มันเพียงแค่สลับและชาร์จ นั่นคือประจุไฟฟ้าเคลื่อนที่และกระแสในวงจรภายนอกคือ บำรุงรักษา
จากทฤษฎีของ Maxwell ในกรณีนี้ เราสามารถพูดได้ว่ากระแสไฟฟ้าสลับภายในตัวเก็บประจุยังคงปิดอยู่ เฉพาะในกรณีนี้เท่านั้น โดยกระแสไบอัส นั่นหมายความว่าตัวเก็บประจุในวงจรไฟฟ้ากระแสสลับทำหน้าที่เป็นตัวต้านทานแบบค่าจำกัดชนิดหนึ่ง แนวต้านนี้เรียกว่า ความจุ.

ในทางปฏิบัติแสดงให้เห็นมานานแล้วว่าปริมาณของกระแสสลับที่ไหลผ่านตัวนำนั้นขึ้นอยู่กับรูปร่างของตัวนำนั้นและคุณสมบัติทางแม่เหล็กของตัวกลางที่อยู่รอบๆด้วยลวดตรงกระแสจะใหญ่ที่สุดและหากลวดเส้นเดียวกันพันเข้ากับขดลวดที่มีจำนวนรอบมากกระแสก็จะน้อยลง
และถ้านำแกนเฟอร์โรแมกเนติกมารวมไว้ในขดลวดเดียวกัน กระแสก็จะยิ่งลดลงไปอีก ดังนั้น สายไฟจึงให้กระแสสลับไม่เพียงแต่มีความต้านทานแบบโอห์มมิก (แอกทีฟ) เท่านั้น แต่ยังมีความต้านทานเพิ่มเติมขึ้นอยู่กับความเหนี่ยวนำของสายไฟด้วย ความต้านทานนี้เรียกว่า อุปนัย.
ความหมายทางกายภาพของมันคือกระแสที่เปลี่ยนแปลงในตัวนำของตัวเหนี่ยวนำบางตัวจะเริ่มต้น EMF ของการเหนี่ยวนำตัวเองในตัวนำนั้น ซึ่งมีแนวโน้มที่จะป้องกันการเปลี่ยนแปลงของกระแส นั่นคือ มีแนวโน้มที่จะลดกระแส ซึ่งเทียบเท่ากับการเพิ่มความต้านทานของลวด
ความจุในวงจรไฟฟ้ากระแสสลับ
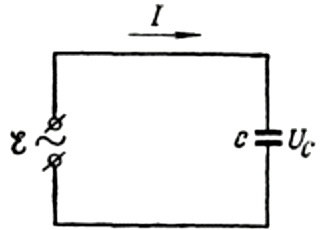
ก่อนอื่นเรามาพูดถึงรายละเอียดเพิ่มเติมเกี่ยวกับความต้านทานแบบ capacitive สมมติว่าตัวเก็บประจุของความจุ C เชื่อมต่อกับแหล่งกระแสสลับไซน์ ดังนั้น EMF ของแหล่งนี้จะอธิบายด้วยสูตรต่อไปนี้:
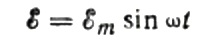
เราจะเพิกเฉยต่อแรงดันไฟตกคร่อมสายเชื่อมต่อ เนื่องจากโดยปกติแล้วจะมีขนาดเล็กมากและสามารถพิจารณาแยกกันได้หากจำเป็น สมมติว่าแรงดันไฟฟ้าทั่วแผ่นตัวเก็บประจุมีค่าเท่ากับแรงดันไฟฟ้าของแหล่งกำเนิดไฟฟ้ากระแสสลับ แล้ว:
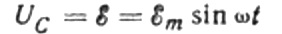
ในช่วงเวลาใดก็ตาม ประจุของตัวเก็บประจุจะขึ้นอยู่กับความจุและแรงดันระหว่างเพลตของมัน จากนั้น เมื่อได้รับแหล่งที่มาที่รู้จักซึ่งได้กล่าวถึงข้างต้น เราได้นิพจน์สำหรับการค้นหาประจุบนแผ่นตัวเก็บประจุด้วยแรงดันไฟฟ้าของแหล่งกำเนิด:
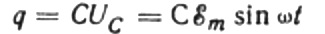
ให้เวลาน้อยที่สุด dt ประจุบนตัวเก็บประจุเปลี่ยนแปลงโดย dq จากนั้นกระแส ฉันจะไหลผ่านสายไฟจากแหล่งจ่ายไปยังตัวเก็บประจุเท่ากับ:
ค่าของแอมพลิจูดปัจจุบันจะเท่ากับ:
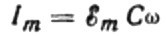
จากนั้นนิพจน์สุดท้ายสำหรับปัจจุบันจะเป็น:
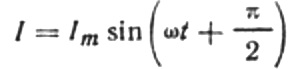
ลองเขียนสูตรแอมพลิจูดปัจจุบันใหม่ดังนี้:
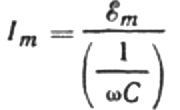
อัตราส่วนนี้เป็นกฎของโอห์ม โดยที่ค่าส่วนกลับของผลคูณของความถี่เชิงมุมและค่าความจุมีบทบาทในการต้านทาน และเป็นนิพจน์สำหรับการค้นหาค่าความจุของตัวเก็บประจุในวงจรไฟฟ้ากระแสสลับแบบไซน์:
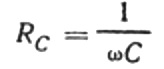
ซึ่งหมายความว่าความต้านทานของตัวเก็บประจุจะแปรผกผันกับความถี่เชิงมุมของกระแสและความจุของตัวเก็บประจุ มันง่ายที่จะเข้าใจความหมายทางกายภาพของการพึ่งพาอาศัยกันนี้
ยิ่งความจุของตัวเก็บประจุในวงจรไฟฟ้ากระแสสลับมีขนาดใหญ่ขึ้นและทิศทางของกระแสในวงจรนั้นเปลี่ยนแปลงบ่อยขึ้น ในที่สุด ประจุทั้งหมดจะผ่านต่อหน่วยเวลามากขึ้นผ่านส่วนตัดขวางของสายไฟที่เชื่อมต่อตัวเก็บประจุกับแหล่งจ่ายกระแสสลับ ซึ่งหมายความว่ากระแสเป็นสัดส่วนกับผลคูณของความจุและความถี่เชิงมุม
ตัวอย่างเช่น ลองคำนวณความจุของตัวเก็บประจุที่มีความจุไฟฟ้า 10 ไมโครฟารัดสำหรับวงจรกระแสสลับไซน์ที่มีความถี่ 50 Hz:
หากความถี่คือ 5,000 Hz ตัวเก็บประจุตัวเดียวกันจะมีความต้านทานประมาณ 3 โอห์ม
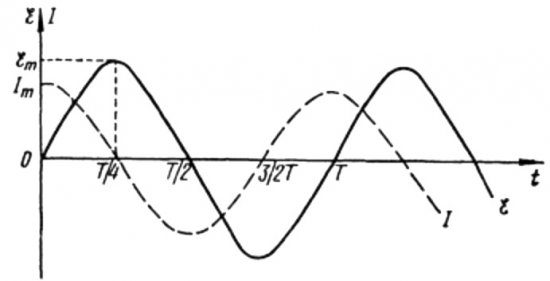
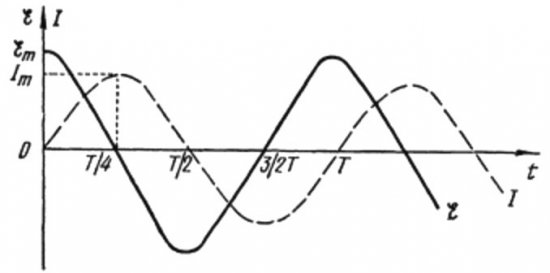
จากสูตรข้างต้นเป็นที่ชัดเจนว่ากระแสและแรงดันในวงจรไฟฟ้ากระแสสลับที่มีตัวเก็บประจุจะเปลี่ยนเฟสต่างๆ เสมอ เฟสปัจจุบันนำไปสู่เฟสแรงดันไฟฟ้าโดย pi / 2 (90 องศา) ซึ่งหมายความว่ากระแสสูงสุดในเวลาจะมีอยู่ก่อนหนึ่งในสี่ของช่วงเวลาก่อนหน้าแรงดันสูงสุดเสมอ ดังนั้น ทั่วทั้งความต้านทานแบบคาปาซิทีฟ กระแสจะนำแรงดันไฟฟ้าไปหนึ่งในสี่ของช่วงเวลา หรือ 90 องศาในเฟส
ให้เราอธิบายความหมายทางกายภาพของปรากฏการณ์นี้ในช่วงเวลาแรก ตัวเก็บประจุจะถูกคายประจุจนหมด ดังนั้นแรงดันไฟฟ้าที่น้อยที่สุดที่ใช้กับตัวเก็บประจุจะเคลื่อนประจุบนแผ่นของตัวเก็บประจุ ทำให้เกิดกระแส
ขณะที่ประจุไฟฟ้าของตัวเก็บประจุ แรงดันไฟฟ้าทั่วทั้งเพลตจะเพิ่มขึ้น สิ่งนี้จะป้องกันการไหลของประจุต่อไป ดังนั้นกระแสในวงจรจึงลดลงแม้ว่าแรงดันไฟฟ้าที่ใช้กับเพลตจะเพิ่มขึ้นอีกก็ตาม
ซึ่งหมายความว่าหากในช่วงเวลาเริ่มต้นกระแสสูงสุด เมื่อแรงดันไฟฟ้าถึงค่าสูงสุดหลังจากช่วงหนึ่งในสี่ กระแสจะหยุดลงอย่างสมบูรณ์
ในช่วงเริ่มต้นของช่วงเวลา กระแสจะสูงสุดและแรงดันจะต่ำสุดและเริ่มเพิ่มขึ้น แต่หลังจากหนึ่งในสี่ของช่วงเวลา แรงดันจะถึงค่าสูงสุด แต่กระแสได้ลดลงถึงศูนย์แล้วในเวลานี้ ดังนั้นปรากฎว่าแรงดันไฟฟ้านำไปสู่แรงดันไฟฟ้าหนึ่งในสี่ของช่วงเวลา
ความต้านทานไฟฟ้ากระแสสลับ
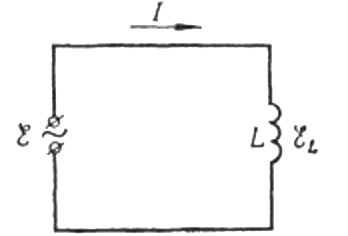
ตอนนี้กลับไปที่ความต้านทานแบบอุปนัย สมมติว่ากระแสสลับไซน์ไหลผ่านขดลวดเหนี่ยวนำ สามารถแสดงเป็น:
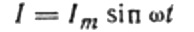
กระแสเกิดจากแรงดันไฟสลับที่ใช้กับขดลวด ซึ่งหมายความว่า EMF ของการเหนี่ยวนำตัวเองจะปรากฏบนขดลวด ซึ่งแสดงได้ดังนี้:
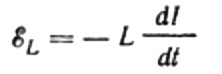
อีกครั้ง เราละเลยแรงดันตกคร่อมสายไฟที่เชื่อมต่อแหล่ง EMF กับขดลวด ความต้านทานโอห์มมิกต่ำมาก
ให้แรงดันไฟฟ้ากระแสสลับที่ใช้กับขดลวด ณ ช่วงเวลาใดเวลาหนึ่งสมดุลอย่างสมบูรณ์โดย EMF ที่เกิดขึ้นของการเหนี่ยวนำตัวเองที่มีขนาดเท่ากันแต่มีทิศทางตรงกันข้าม:
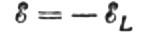
จากนั้นเรามีสิทธิ์ที่จะเขียน:
เนื่องจากแอมพลิจูดของแรงดันไฟฟ้าที่ใช้กับขดลวดคือ:
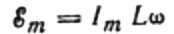
เราได้รับ:
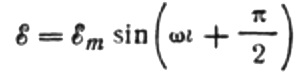
ให้เราแสดงกระแสสูงสุดดังนี้:
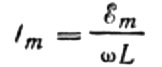
นิพจน์นี้เป็นกฎของโอห์มเป็นหลัก ปริมาณที่เท่ากับผลคูณของตัวเหนี่ยวนำและความถี่เชิงมุมมีบทบาทในการต้านทานที่นี่ และไม่มีอะไรมากไปกว่าความต้านทานเชิงอุปนัยของตัวเหนี่ยวนำ:

ดังนั้น ความต้านทานแบบเหนี่ยวนำจะเป็นสัดส่วนกับความเหนี่ยวนำของขดลวดและความถี่เชิงมุมของกระแสสลับที่ผ่านขดลวดนั้น
นี่เป็นเพราะความจริงที่ว่าความต้านทานอุปนัยนั้นเกิดจากอิทธิพลของ EMF ที่เหนี่ยวนำตัวเองต่อแรงดันไฟฟ้าแหล่งที่มา - EMF ที่เหนี่ยวนำตัวเองมีแนวโน้มที่จะลดกระแสและทำให้วงจรมีความต้านทาน ดังที่ทราบกันดีว่าขนาดของแรงเคลื่อนไฟฟ้าของการเหนี่ยวนำตัวเองนั้นเป็นสัดส่วนกับความเหนี่ยวนำของขดลวดและอัตราการเปลี่ยนแปลงของกระแสที่ไหลผ่าน
ตัวอย่างเช่น ลองคำนวณความต้านทานแบบเหนี่ยวนำของขดลวดที่มีค่าความเหนี่ยวนำ 1 H ซึ่งรวมอยู่ในวงจรที่มีความถี่ปัจจุบัน 50 Hz:
หากความถี่ของลูกบอลคือ 5,000 Hz ความต้านทานของขดลวดเดียวกันจะอยู่ที่ประมาณ 31,400 โอห์ม จำได้ว่าความต้านทานโอห์มมิกของขดลวดมักจะไม่กี่โอห์ม
จากสูตรข้างต้น เห็นได้ชัดว่าการเปลี่ยนแปลงของกระแสผ่านขดลวดและแรงดันที่เกิดขึ้นในเฟสต่างๆ และเฟสของกระแสจะน้อยกว่าเฟสของแรงดันที่ pi / 2 เสมอ ดังนั้น กระแสสูงสุดเกิดขึ้นหนึ่งไตรมาสหลังจากเริ่มเกิดความเครียดสูงสุด
ในการต้านทานแบบเหนี่ยวนำ กระแสจะหน่วงแรงดันไฟฟ้าลง 90 องศาเนื่องจากผลการเบรกของ EMF ที่เหนี่ยวนำตัวเอง ซึ่งป้องกันไม่ให้กระแสเปลี่ยนแปลง (ทั้งเพิ่มขึ้นและลดลง) ดังนั้นกระแสสูงสุดจึงถูกสังเกตในวงจรด้วยขดลวดในภายหลัง กว่าแรงดันไฟฟ้าสูงสุด
การทำงานของคอยล์และตัวเก็บประจุรวมกัน
หากคุณเชื่อมต่อขดลวดกับตัวเก็บประจุแบบอนุกรมกับวงจรไฟฟ้ากระแสสลับ แรงดันไฟฟ้าของขดลวดจะเลื่อนแรงดันไฟฟ้าของตัวเก็บประจุให้ทันเวลาครึ่งหนึ่ง นั่นคือ 180 องศาในเฟส
เรียกการต้านทานแบบคาปาซิทีฟและอุปนัย สารตั้งต้น… พลังงานจะไม่ถูกใช้ไปในการต้านทานปฏิกิริยาเช่นเดียวกับการต้านทานแบบแอคทีฟ พลังงานที่เก็บไว้ในตัวเก็บประจุจะถูกส่งกลับไปยังแหล่งกำเนิดเป็นระยะเมื่อสนามไฟฟ้าในตัวเก็บประจุหายไป
เช่นเดียวกับขดลวด: เนื่องจากสนามแม่เหล็กของขดลวดถูกสร้างขึ้นโดยกระแส พลังงานในขดลวดจะสะสมในช่วงหนึ่งในสี่ของช่วงเวลา และในช่วงไตรมาสถัดไปของช่วงเวลา พลังงานจะกลับสู่แหล่งกำเนิด ในบทความนี้เราได้พูดถึงกระแสสลับไซน์ซึ่งปฏิบัติตามกฎระเบียบเหล่านี้อย่างเคร่งครัด
ในวงจรไฟฟ้ากระแสสลับแบบไซน์ จะเรียกตัวเหนี่ยวนำแบบคอร์ หายใจไม่ออกมักใช้สำหรับการจำกัดกระแส ข้อได้เปรียบเหนือรีโอสแตทคือพลังงานไม่กระจายเป็นความร้อนในปริมาณมหาศาล