โหมดการทำงานของหม้อแปลง

หม้อแปลงสามารถทำงานได้ในสามโหมดทั้งนี้ขึ้นอยู่กับค่าของโหลด:

1. การทำงานที่ไม่ได้ใช้งานที่ความต้านทานโหลด zn = ∞

2. ไฟฟ้าลัดวงจรที่ zn = 0

3. โหมดการชาร์จที่ 0 <zn <∞

ด้วยพารามิเตอร์ของวงจรสมมูล คุณสามารถวิเคราะห์โหมดการทำงานใดๆ ของหม้อแปลง... พารามิเตอร์ต่างๆ ที่ไม่ได้ใช้งาน ขดลวดทุติยภูมิของหม้อแปลงเปิดอยู่

การทดสอบหม้อแปลงไฟฟ้าแบบไม่โหลดจะดำเนินการเพื่อกำหนดอัตราส่วนการเปลี่ยนแปลง การสูญเสียพลังงานในเหล็กและพารามิเตอร์ของสาขาแม่เหล็กของวงจรสมมูล ซึ่งมักจะดำเนินการที่แรงดันไฟฟ้าที่กำหนดของขดลวดปฐมภูมิ

สำหรับ หม้อแปลงเฟสเดียว ขึ้นอยู่กับข้อมูลจากการทดสอบที่ไม่ได้ใช้งาน เป็นไปได้ที่จะคำนวณ:

— ปัจจัยการเปลี่ยนแปลง

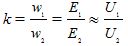
— เปอร์เซ็นต์ของกระแสที่ไม่มีโหลด

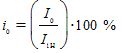
คือความต้านทานที่ใช้งานของการสะกดจิตสาขา r0 ที่กำหนดโดยเงื่อนไข

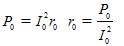
— ความต้านทานรวมของสาขาแม่เหล็ก

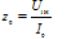
— ความต้านทานแบบเหนี่ยวนำของสาขาแม่เหล็ก

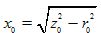
ตัวประกอบกำลังที่ไม่ได้ใช้งานมักถูกกำหนดเป็น:

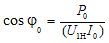
ในบางกรณี การทดสอบแบบไม่โหลดจะดำเนินการสำหรับค่าต่างๆ ของแรงดันไฟฟ้าที่คดเคี้ยวหลัก: จาก U1 ≈ 0.3U1n ถึง U1 ≈ 1.1U1n จากข้อมูลที่ได้รับจะมีการวาดลักษณะที่ไม่ได้ใช้งานซึ่งขึ้นอยู่กับ P0, z0, r0 และcosφเป็นฟังก์ชันของแรงดันไฟฟ้า U1 การใช้คุณสมบัติไม่โหลดทำให้สามารถตั้งค่าของปริมาณที่ระบุที่ค่าใด ๆ ของแรงดันไฟฟ้า U1

ในการพิจารณาแรงดันไฟฟ้าลัดวงจร การสูญเสียในขดลวดและความต้านทาน rk และ xk จะถูกทดสอบในการลัดวงจร ในกรณีนี้แรงดันไฟฟ้าที่ลดลงจะถูกนำไปใช้กับขดลวดปฐมภูมิเพื่อให้กระแสของขดลวดหม้อแปลงลัดวงจรมีค่าเท่ากับค่าเล็กน้อยเช่น I1k = I1n, I2k = I2n แรงดันไฟฟ้าของขดลวดปฐมภูมิที่ตรงตามเงื่อนไขที่กำหนดเรียกว่า แรงดันไฟฟ้าลัดวงจรที่ระบุ Ukn

เนื่องจากโดยปกติแล้ว Ucn จะมีค่าเพียง 5-10% ของ U1n ฟลักซ์การเหนี่ยวนำร่วมกันของแกนหม้อแปลงระหว่างการทดสอบการลัดวงจรจึงน้อยกว่าโหมดปกติหลายสิบเท่า และเหล็กของหม้อแปลงจะไม่อิ่มตัว ดังนั้นการสูญเสียในเหล็กจึงถูกละเลยและถือว่าพลังงาน Pcn ทั้งหมดที่จ่ายให้กับขดลวดปฐมภูมิถูกใช้ไปเพื่อให้ความร้อนแก่ขดลวดและกำหนดค่าของความต้านทานการลัดวงจรที่ใช้งานอยู่ rc

ในระหว่างการทดลอง วัดแรงดัน Ukn, I1k ปัจจุบัน = I1n และกำลัง Pkn ของขดลวดปฐมภูมิ จากข้อมูลนี้ คุณสามารถระบุได้ว่า:

— เปอร์เซ็นต์ของแรงดันลัดวงจร

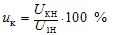
- ความต้านทานไฟฟ้าลัดวงจรที่ใช้งานอยู่

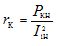
— ความต้านทานแบบแอคทีฟของขดลวดปฐมภูมิและขดลวดทุติยภูมิลดลง ประมาณเท่ากับครึ่งหนึ่งของความต้านทานไฟฟ้าลัดวงจร

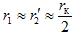
- ความต้านทานไฟฟ้าลัดวงจร

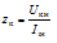
- ความต้านทานไฟฟ้าลัดวงจร

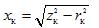
— ความต้านทานอุปนัยของขดลวดปฐมภูมิและขดลวดทุติยภูมิลดลง ประมาณเท่ากับครึ่งหนึ่งของความต้านทานอุปนัยไฟฟ้าลัดวงจร

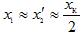
— ความต้านทานของขดลวดทุติยภูมิของหม้อแปลงจริง:

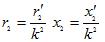
— แรงดันลัดวงจรอุปนัย แอกทีฟ และเปอร์เซ็นต์ทั้งหมด:

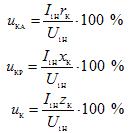
โหมดโหลด V เป็นสิ่งสำคัญมากที่จะต้องรู้ว่าพารามิเตอร์โหลดส่งผลต่อประสิทธิภาพและความผันแปรของแรงดันไฟฟ้าที่ขั้วของขดลวดทุติยภูมิอย่างไร

ประสิทธิภาพของหม้อแปลงคืออัตราส่วนของพลังงานที่ใช้งานที่ส่งไปยังโหลดต่อพลังงานที่ใช้งานที่จ่ายให้กับหม้อแปลง

ประสิทธิภาพของหม้อแปลงมีความสำคัญอย่างยิ่ง สำหรับหม้อแปลงพลังงานต่ำมีค่าประมาณ 0.95 และสำหรับหม้อแปลงที่มีความจุหลายหมื่นกิโลโวลต์แอมแปร์จะสูงถึง 0.995

การกำหนดประสิทธิภาพตามสูตรโดยใช้กำลังที่วัดได้โดยตรง P1 และ P2 ทำให้เกิดข้อผิดพลาดมาก สะดวกกว่าที่จะนำเสนอสูตรนี้ในรูปแบบอื่น:

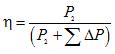
ผลรวมของการสูญเสียในหม้อแปลงอยู่ที่ไหน

การสูญเสียในหม้อแปลงมีอยู่สองประเภท: การสูญเสียทางแม่เหล็กที่เกิดจากการผ่านของฟลักซ์แม่เหล็กผ่านวงจรแม่เหล็ก และการสูญเสียทางไฟฟ้าที่เกิดจากการไหลของกระแสผ่านขดลวด

เนื่องจากฟลักซ์แม่เหล็กของหม้อแปลงที่ U1 = const และการเปลี่ยนแปลงของกระแสทุติยภูมิจากศูนย์เป็นค่าเล็กน้อยยังคงที่ ดังนั้นการสูญเสียสนามแม่เหล็กในช่วงโหลดนี้จึงถือว่าคงที่และเท่ากับการสูญเสียที่ไม่มีโหลด

การสูญเสียทางไฟฟ้าในทองแดงของขดลวด ∆Pm เป็นสัดส่วนกับกำลังสองของกระแสไฟฟ้า สะดวกที่จะแสดงเป็นการสูญเสียจากไฟฟ้าลัดวงจร Pcn ที่ได้รับกระแสไฟฟ้าที่กำหนด

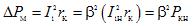
โดยที่ β เป็นตัวประกอบภาระ

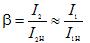
สูตรการคำนวณเพื่อหาประสิทธิภาพของหม้อแปลง:

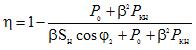
โดยที่ Sn คือกำลังที่ชัดเจนของหม้อแปลง φ2 คือมุมเฟสระหว่างแรงดันและกระแสในโหลด

สามารถหาประสิทธิภาพสูงสุดได้โดยการเทียบอนุพันธ์อันดับหนึ่งกับศูนย์ ในกรณีนี้ เราพบว่าประสิทธิภาพมีค่าสูงสุดที่โหลดดังกล่าวเมื่อการสูญเสียค่าคงที่ (ไม่ขึ้นกับกระแส) P0 เท่ากับการสูญเสียแบบสลับ (ขึ้นอยู่กับกระแส) ดังนั้น

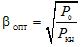
สำหรับหม้อแปลงน้ำมันกำลังสมัยใหม่ βopt = 0.5 — 0.7 เมื่อโหลดดังกล่าวหม้อแปลงมักจะทำงานระหว่างการใช้งาน

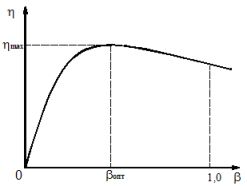
กราฟของการพึ่งพา η = f (β) แสดงในรูปที่ 1

รูปที่ 1. เส้นโค้งของการเปลี่ยนแปลงประสิทธิภาพของหม้อแปลงขึ้นอยู่กับโหลดแฟกเตอร์

ในการกำหนดเปอร์เซ็นต์การเปลี่ยนแปลงของแรงดันทุติยภูมิของหม้อแปลงเฟสเดียว ให้ใช้สมการ

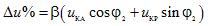
โดยที่ uKA และ ukR เป็นส่วนประกอบที่ใช้งานและเกิดปฏิกิริยาของแรงดันไฟลัดวงจร ซึ่งแสดงเป็นเปอร์เซ็นต์

การเปลี่ยนแปลงของแรงดันหม้อแปลงขึ้นอยู่กับโหลดแฟคเตอร์ (β) ลักษณะของมัน (มุม φ2) และส่วนประกอบของแรงดันลัดวงจร (uKA และ uKR)

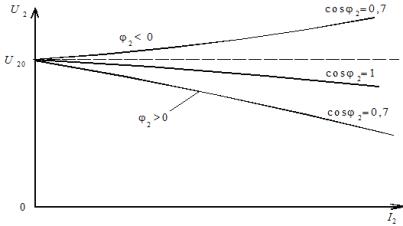
ลักษณะภายนอกของหม้อแปลง คือการพึ่งพาที่ U1 = const และ cosφ2 = const (รูปที่ 2)

รูปที่ 2 ลักษณะภายนอกของหม้อแปลงกำลังปานกลางและสูงสำหรับโหลดประเภทต่างๆ