ความเป็นฉนวนของฉนวน ตัวอย่างการคำนวณ

เมื่อแรงดันไฟฟ้า U เพิ่มขึ้นทีละน้อยระหว่างตัวนำที่คั่นด้วยไดอิเล็กตริก (ฉนวน) ตัวอย่างเช่น แผ่นตัวเก็บประจุหรือสายไฟที่เป็นตัวนำ ความเข้ม (ความแรง) ของสนามไฟฟ้าในไดอิเล็กตริกจะเพิ่มขึ้น ความแรงของสนามไฟฟ้าในไดอิเล็กตริกก็เพิ่มขึ้นเช่นกันเมื่อระยะห่างระหว่างสายลดลง

ที่ความแรงของสนามไฟฟ้า การสลายตัวเกิดขึ้นในไดอิเล็กตริก เกิดประกายไฟหรือส่วนโค้งขึ้น และกระแสไฟฟ้าจะปรากฏขึ้นในวงจร ความแรงของสนามไฟฟ้าที่เกิดการแตกตัวของฉนวนเรียกว่า ความแรงไฟฟ้า Epr ของฉนวน

ความเป็นฉนวนหมายถึงแรงดันไฟฟ้าต่อมิลลิเมตรของความหนาของฉนวนและวัดเป็น V/mm (kV/mm) หรือ kV/cm ตัวอย่างเช่น ความเป็นฉนวนของอากาศระหว่างแผ่นเรียบคือ 32 kV / cm

ความแรงของสนามไฟฟ้าในไดอิเล็กตริกสำหรับกรณีที่ตัวนำอยู่ในรูปของแผ่นหรือแถบคั่นด้วยช่องว่างที่เท่ากัน (เช่น ในตัวเก็บประจุแบบกระดาษ) คำนวณโดยสูตร

E = U / d,

โดยที่ U คือแรงดันไฟฟ้าระหว่างสายไฟ V (kV); d — ความหนาของชั้นอิเล็กทริก mm (ซม.)

ตัวอย่างของ

1. ความแรงของสนามไฟฟ้าในช่องว่างอากาศหนา 3 ซม. ระหว่างแผ่นเป็นเท่าใดถ้าแรงดันไฟฟ้าระหว่างแผ่นเป็น U = 100 kV (รูปที่ 1)

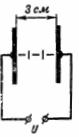
ข้าว. 1.

ความแรงของสนามไฟฟ้าคือ: E = U / d = 100000/3 = 33333 V / cm.

แรงดันไฟฟ้าดังกล่าวเกินความเป็นฉนวนของอากาศ (32 kV / cm) และมีความเสี่ยงที่จะถูกทำลาย

ความเสี่ยงของความเสียหายของไฟฟ้ากระแสตรงสามารถป้องกันได้โดยการเพิ่มช่องว่าง เช่น 5 ซม. หรือโดยใช้ฉนวนอื่นที่แข็งแรงกว่าแทนอากาศ เช่น กระดาษแข็งไฟฟ้า (รูปที่ 2)

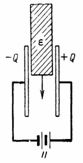
ข้าว. 2.

กระดาษแข็งไฟฟ้ามีค่าคงที่ไดอิเล็กตริก ε = 2 และความเป็นไดอิเล็กตริก 80,000 V/ซม. ในกรณีของเรา ความแรงของสนามไฟฟ้าในฉนวนคือ 33333 V อากาศไม่สามารถต้านทานแรงนี้ได้ ในขณะที่กระดาษแข็งไฟฟ้าในกรณีนี้มีค่าความเป็นฉนวนสำรองอยู่ที่ 80,000/33333 = 2.4 เนื่องจากความเป็นฉนวนของกล่องไฟฟ้าคือ 80,000/32,000 = 2.5 เท่าของอากาศ

2. ความแรงของสนามไฟฟ้าในไดอิเล็กตริกของตัวเก็บประจุหนา 3 มม. เป็นเท่าใดหากต่อตัวเก็บประจุกับแรงดันไฟฟ้า U = 6 kV

E = U / d = 6000 / 0.3 = 20,000 V / ซม.

3. อิเล็กทริกที่มีความหนา 2 มม. แตกตัวที่แรงดัน 30 kV ความแรงของไฟฟ้าคืออะไร?

E = U / d = 30,000 / 0.2 = 150,000 V / cm = 150 kV / cm. แก้วมีความแข็งแรงทางไฟฟ้า

4. ช่องว่างระหว่างแผ่นของตัวเก็บประจุเต็มไปด้วยชั้นของกระดาษแข็งไฟฟ้าและชั้นไมกาที่มีความหนาเท่ากัน (รูปที่ 3) แรงดันไฟฟ้าระหว่างแผ่นของตัวเก็บประจุคือ U = 10,000 V กระดาษแข็งไฟฟ้ามีค่าคงที่ไดอิเล็กทริก ε1 = 2 และไมกา ε2 = 8แรงดันไฟฟ้า U จะกระจายอย่างไรระหว่างชั้นของฉนวนและสนามไฟฟ้าในแต่ละชั้นจะมีความเข้มเท่าใด

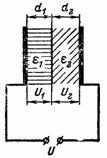
ข้าว. 3.

แรงดันไฟฟ้า U1 และ U2 ในชั้นอิเล็กทริกที่มีความหนาเท่ากันจะไม่เท่ากัน แรงดันไฟฟ้าของตัวเก็บประจุจะถูกแบ่งออกเป็นแรงดันไฟฟ้า U1 และ U2 ซึ่งจะแปรผกผันกับค่าคงที่ไดอิเล็กตริก:

U1 / U2 = ε2 / ε1 = 8/2 = 4/1 = 4;

U1 = 4 ∙ U2

เนื่องจาก U = U1 + U2 เรามีสมการสองสมการที่มีนิรนามสองตัว

แทนสมการแรกลงในสมการที่สอง: U = 4 ∙ U2 + U2 = 5 ∙ U2

ดังนั้น 10,000 V = 5 ∙ U2; U2 = 2,000 V; U1 = 4, U2 = 8000V.

แม้ว่าชั้นอิเล็กทริกจะมีความหนาเท่ากัน แต่ก็มีประจุไม่เท่ากัน ไดอิเล็กตริกที่มีค่าคงที่ไดอิเล็กตริกสูงกว่าจะโหลดน้อยกว่า (U2 = 2000 V) และในทางกลับกัน (U1 = 8000 V)

ความแรงของสนามไฟฟ้า E ในชั้นอิเล็กทริกเท่ากับ:

E1 = U1 / d1 = 8000 / 0.2 = 40,000 V / cm;

E2 = U2 / d2 = 2,000 / 0.2 = 10,000 V / ซม.

ความแตกต่างของค่าคงที่ไดอิเล็กตริกทำให้ความแรงของสนามไฟฟ้าเพิ่มขึ้น หากช่องว่างทั้งหมดเต็มไปด้วยไดอิเล็กตริกเพียงอันเดียว เช่น ไมกาหรือกระดาษแข็งไฟฟ้า ความแรงของสนามไฟฟ้าจะน้อยลง เนื่องจากมันจะกระจายอย่างเท่าเทียมกันในช่องว่าง:

E = U / d = (U1 + U2) / (d1 + d2) = 10,000 / 0.4 = 25,000 V / ซม.

ดังนั้นจึงจำเป็นต้องหลีกเลี่ยงการใช้ฉนวนที่ซับซ้อนซึ่งมีค่าคงที่ไดอิเล็กตริกต่างกันมาก ด้วยเหตุผลเดียวกัน ความเสี่ยงของความล้มเหลวจะเพิ่มขึ้นเมื่อมีฟองอากาศก่อตัวขึ้นในฉนวน

5. หาความแรงของสนามไฟฟ้าในไดอิเล็กตริกของตัวเก็บประจุจากตัวอย่างที่แล้วหากความหนาของชั้นไดอิเล็กตริกไม่เท่ากันแผ่นไฟฟ้ามีความหนา d1 = 0.2 มม. และไมกา d2 = 3.8 มม. (รูปที่ 4)

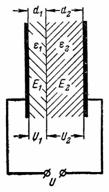
ข้าว. 4.

ความแรงของสนามไฟฟ้าจะกระจายผกผันกับค่าคงที่ไดอิเล็กตริก:

E1 / E2 = ε2 / ε1 = 8/2 = 4

เนื่องจาก E1 = U1 / d1 = U1 / 0.2 และ E2 = U2 / d2 = U2 / 3.8 ดังนั้น E1 / E2 = (U1 / 0.2) / (U2 / 3.8) = (U1 ∙ 3.8) / (0.2 ∙ U2) = 19 ∙ U1 / U2.

ดังนั้น E1 / E2 = 4 = 19 ∙ U1 / U2 หรือ U1 / U2 = 4/19

ผลรวมของแรงดัน U1 และ U2 บนชั้นอิเล็กทริกเท่ากับแรงดันแหล่งที่มา U: U = U1 + U2; 10,000 = U1 + U2

เนื่องจาก U1 = 4/19 ∙ U2 ดังนั้น 10,000 = 4/10 ∙ U2 + U2 = 23/19 ∙ U2; U2 = 190,000 /23 = 8260 V; U1 = U-U2 = 1740V.

ความแรงของสนามไฟฟ้าในไมกาคือ E2 ∙ 8260 / 3.8≈2174 V / cm.

ไมก้ามีความแข็งแรงทางไฟฟ้า 80,000 V / mm และสามารถทนต่อแรงดันไฟฟ้าดังกล่าวได้

ความแรงของสนามไฟฟ้าในกระดาษแข็งไฟฟ้าคือ E1 = 1740 / 0.2 = 8700 V / mm.

กระดาษแข็งไฟฟ้าจะไม่ทนต่อแรงดันไฟฟ้าดังกล่าวเนื่องจากความเป็นฉนวนเพียง 8000 V / mm.

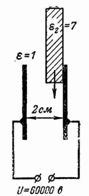
6. ต่อแรงดันไฟฟ้า 60,000 V เข้ากับแผ่นโลหะสองแผ่นห่างกัน 2 ซม. จงหาความแรงของสนามไฟฟ้าในช่องว่างอากาศรวมทั้งความแรงของสนามไฟฟ้าในอากาศและกระจกถ้ามีกระจกอยู่ในช่องว่างให้ใส่แผ่นด้วย ความหนา 1 ซม. (รูปที่ 5)

ข้าว. 5.

ถ้ามีเพียงอากาศระหว่างแผ่นเปลือกโลก ความแรงของสนามไฟฟ้าในนั้นจะเท่ากับ: E = U / d = 60,000 /2 = 30,000 V / cm.

ความแรงของสนามใกล้เคียงกับความเป็นฉนวนของอากาศหากใส่แผ่นกระจกหนา 1 ซม. (ค่าคงที่ไดอิเล็กตริกแก้ว ε2 = 7) ลงในช่องว่าง E1 = U1 / d1 = U1 / 1 = U1 E2 = U2 / d2 = U2 / 1 = U2; E1 / E2 = ε2 / ε1 = 7/1 = U1 / U2;

U1 = 7 ∙ U2; U1 = 60,000-U2; 8 ∙ U2 = 60,000; U2 = 7500 V; E2 = U2 / d2 = 7500 โวลต์ / ซม.

ความแรงของสนามไฟฟ้าในแก้วคือ E2 = 7.5 kV / cm และความแรงของไฟฟ้าคือ 150 kV / cm

ในกรณีนี้ กระจกมีปัจจัยด้านความปลอดภัย 20 เท่า

สำหรับช่องว่างอากาศที่เรามี: U1 = 60,000-7500 = 52500 V; E1 = U1 / d1 = 52500 V / cm.

ในกรณีนี้ความแรงของสนามไฟฟ้าในช่องว่างอากาศจะมากกว่าสนามแรกโดยไม่มีกระจก หลังจากใส่แก้วแล้ว ส่วนผสมทั้งหมดจะมีความแข็งแรงน้อยกว่าอากาศเพียงอย่างเดียว

ความเสี่ยงของการแตกหักยังเกิดขึ้นเมื่อความหนาของแผ่นกระจกเท่ากับช่องว่างระหว่างแผ่นนำไฟฟ้า เช่น 2 ซม. เนื่องจากจะมีช่องว่างอากาศบาง ๆ ในช่องว่างที่จะถูกเจาะอย่างหลีกเลี่ยงไม่ได้

ความเป็นไดอิเล็กตริกของช่องว่างระหว่างตัวนำไฟฟ้าแรงสูงต้องเสริมด้วยวัสดุที่มีค่าคงที่ไดอิเล็กตริกต่ำและความเป็นไดอิเล็กตริกสูง เช่น กระดาษแข็งไฟฟ้าที่มีค่า ε = 2 หลีกเลี่ยงการผสมวัสดุที่มีค่าคงที่ไดอิเล็กตริกสูง (แก้ว , พอร์ซเลน) และอากาศซึ่งต้องเปลี่ยนน้ำมัน