การคำนวณวงจรแม่เหล็ก

ในเครื่องจักรและอุปกรณ์ไฟฟ้า ฟลักซ์แม่เหล็ก F มีความเข้มข้นในวงจรแม่เหล็ก (แกนแม่เหล็กไฟฟ้า) และช่องว่างอากาศของวงจรแม่เหล็กนี้ เส้นทางของฟลักซ์แม่เหล็กนี้เรียกว่าวงจรแม่เหล็ก

วงจรแม่เหล็กก็เหมือนวงจรไฟฟ้า ฟลักซ์แม่เหล็ก Ф คล้ายกับกระแสไฟฟ้า I การเหนี่ยวนำ В คล้ายกับความหนาแน่นกระแส แรงแม่เหล็ก (ns) Fн (H ∙ l = I ∙ ω) สอดคล้องกับ e เป็นต้น กับ

ในกรณีที่ง่ายที่สุด วงจรแม่เหล็กจะมีหน้าตัดเหมือนกันทุกที่และทำจากวัสดุแม่เหล็กที่เป็นเนื้อเดียวกัน เพื่อกำหนด n เมื่อต้องใช้ l ∙ ω เพื่อให้เกิดการเหนี่ยวนำ B ความเข้มที่สอดคล้องกัน H จะถูกกำหนดจากเส้นโค้งการสะกดจิตและคูณด้วยความยาวเฉลี่ยของเส้นสนามแม่เหล็ก l: H ∙ l = I ∙ ω = Fm

จากที่นี่ กระแสที่ต้องการ I หรือจำนวนรอบ ω ของขดลวดจะถูกกำหนด

วงจรแม่เหล็กที่ซับซ้อนมักมีส่วนที่มีส่วนต่าง ๆ และวัสดุแม่เหล็ก ส่วนเหล่านี้มักจะเชื่อมต่อแบบอนุกรม ดังนั้นฟลักซ์แม่เหล็ก F เดียวกันจึงผ่านแต่ละส่วนการเหนี่ยวนำ B ในแต่ละส่วนขึ้นอยู่กับส่วนตัดขวางของส่วน และคำนวณสำหรับแต่ละส่วนแยกกันโดยใช้สูตร B = Φ∶S

สำหรับค่าการเหนี่ยวนำที่แตกต่างกัน ความเข้ม H จะถูกกำหนดจากเส้นโค้งการดึงดูดและคูณด้วยความยาวเฉลี่ยของสายไฟของส่วนที่สอดคล้องกันของวงจร เมื่อสรุปผลงานแต่ละชิ้น จะได้ n ที่สมบูรณ์ ค. วงจรแม่เหล็ก:

Fm = I ∙ ω = H1 ∙ l1 + H2 ∙ l2 + H3 ∙ l3 + … ซึ่งกำหนดกระแสแม่เหล็กหรือจำนวนรอบของขดลวด

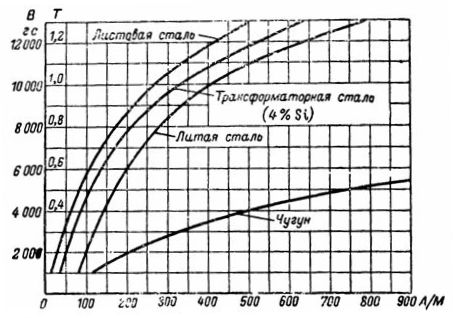
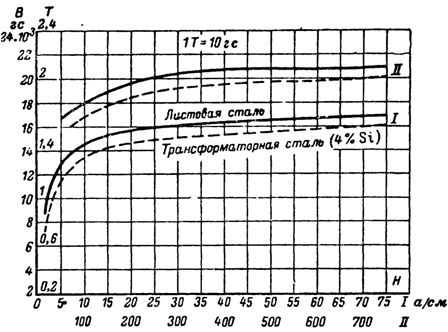
เส้นโค้งการสะกดจิต

ตัวอย่างของ

1. กระแสแม่เหล็ก I ของขดลวด 200 รอบจะต้องเป็นอย่างไรจึงจะ n c. ฟลักซ์แม่เหล็กที่สร้างขึ้นในวงแหวนเหล็ก Ф = 15700 Ms = 0.000157 Wb? รัศมีเฉลี่ยของวงแหวนเหล็กหล่อคือ r = 5 ซม. และเส้นผ่านศูนย์กลางของส่วนคือ d = 2 ซม. (รูปที่ 1)

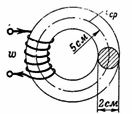
ข้าว. 1.

ส่วนของวงจรแม่เหล็ก S = (π ∙ d ^ 2) / 4 = 3.14 cm2

การเหนี่ยวนำในแกนคือ: B = Φ∶S = 15700∶3.14 = 5,000 G.

ในระบบ MKSA การเหนี่ยวนำคือ: B = 0.000157 Wb: 0.0000314 m2 = 0.5 T

จากเส้นโค้งการทำให้เป็นแม่เหล็กของเหล็กหล่อ เราพบกำลังที่ต้องการ H เท่ากับ 750 A / m สำหรับ B = 5,000 G = 0.5 T ความแรงแม่เหล็กเท่ากับ: I ∙ ω = H ∙ l = 235.5 Av.

ดังนั้นกระแสที่ต้องการ I = (H ∙ l) / ω = 235.5 / 200 = 1.17 A.

2. วงจรแม่เหล็กปิด (รูปที่ 2) ทำจากแผ่นเหล็กของหม้อแปลง ต้องมีกี่รอบในขดลวดที่มีกระแส 0.5 A เพื่อสร้างฟลักซ์แม่เหล็กในแกนกลาง Ф = 160000 Ms = 0.0016 Wb

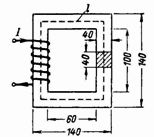
ข้าว. 2.

ส่วนหลัก S = 4 ∙ 4 = 16 cm2 = 0.0016 m2

การเหนี่ยวนำแกน B = F / S = 160000/16 = 10,000 Gs = 1 T

ตามเส้นโค้งการดึงดูดของเหล็กหม้อแปลงเราพบว่าความเข้มของ B = 10,000 Gs = 1 T H = 3.25 A / cm = 325 A / m

ความยาวเฉลี่ยของเส้นสนามแม่เหล็กคือ l = 2 ∙ (60 + 40) + 2 ∙ (100 + 40) = 480 = 0.48 ม.

แรงแม่เหล็ก Fm = I ∙ ω = H ∙ l = 3.25 ∙ 48 = 315 ∙ 0.48 = 156 Av.

ที่กระแส 0.5 A จำนวนรอบคือ ω = 156 / 0.5 = 312

3. วงจรแม่เหล็กที่แสดงในรูป 3 คล้ายกับวงจรแม่เหล็กของตัวอย่างก่อนหน้า ยกเว้นว่ามีช่องว่างอากาศเท่ากับ δ = 5 มม. สิ่งที่ควรจะเป็น s และกระแสขดลวดเพื่อให้ฟลักซ์แม่เหล็กเหมือนกับในตัวอย่างก่อนหน้า นั่นคือ F = 160000 Ms = 0.0016 Wb?

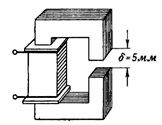
ข้าว. 3.

วงจรแม่เหล็กมีส่วนเชื่อมต่อแบบอนุกรมสองส่วน ซึ่งส่วนตัดขวางจะเหมือนกับในตัวอย่างก่อนหน้า นั่นคือ S = 16 cm2 ความเหนี่ยวนำก็เท่ากับ B = 10,000 G = 1 T

ความยาวเฉลี่ยของเส้นแม่เหล็กเหล็กสั้นกว่าเล็กน้อย: lс = 48-0.5 = 47.5 cm ≈0.48 m.

แรงดันแม่เหล็กในส่วนนี้ของวงจรแม่เหล็กคือ Hc ∙ lc = 3.25 ∙ 48≈156 Av

ความแรงของสนามในช่องว่างอากาศคือ: Hδ = 0.8 ∙ B = 0.8 ∙ 10,000 = 8,000 A / cm.

ความตึงแม่เหล็กในส่วนตัดขวางของช่องว่างอากาศ Hδ ∙ δ = 8000 ∙ 0.5 = 4000 Av.

กรอก n c. เท่ากับผลรวมของแรงดันแม่เหล็กในแต่ละส่วน: I ∙ ω = Hс ∙ lс + Hδ ∙ δ = 156 + 4000 = 4156 Av. ฉัน = (ฉัน ∙ ω) / ω = 4156/312 = 13.3 ก.

หากในตัวอย่างก่อนหน้านี้กระแสไฟฟ้า 0.5 A ที่จำเป็นสำหรับวงจรแม่เหล็กที่มีช่องว่างอากาศ 0.5 ซม. จำเป็นต้องมีกระแส 13 A เพื่อให้ได้ฟลักซ์แม่เหล็กเดียวกัน จากนี้จะเห็นได้ว่าช่องว่างอากาศแม้จะไม่มีนัยสำคัญเมื่อเทียบกับความยาวของวงจรแม่เหล็ก แต่ก็เพิ่ม n ที่ต้องการอย่างมาก v. และกระแสขด.

4. ฟลักซ์แม่เหล็กของหม้อแปลงคำนวณเป็น F = 72000 Ms จำเป็นต้องมีการคำนวณ ns. และกระแสแม่เหล็กของขดลวดปฐมภูมิที่มี 800 รอบ มีช่องว่าง δ = 0.2 มม. ในแกนของหม้อแปลง ขนาดของแกนหม้อแปลงแสดงในรูปที่ 4. ภาพตัดขวางของแกนกลาง S = 2 ∙ 3​ = 6 cm2 (หม้อแปลงที่มีแกนของรูปร่างนี้เรียกว่าหุ้มเกราะ)

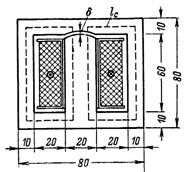
ข้าว. 4.

การเหนี่ยวนำแกนกลางและช่องว่างอากาศ B = F / S = 72000/6 = 12000 G.

ตามเส้นโค้งการดึงดูดของเหล็กหม้อแปลงสำหรับ B = 12,000 G เรากำหนดความเข้ม: Hc = 5 A / cm

ความยาวเฉลี่ยของเส้นแม่เหล็กในเหล็กกล้าคือ lс = 2 ∙ (6 + 3) = 18 ซม.

แรงดันไฟฟ้าในช่องว่างอากาศ Hδ = 0.8 ∙ B = 9600 A / cm.

แรงแม่เหล็ก I ∙ ω = Hc ∙ lc + Hδ ∙ δ = 5 ∙ 18 + 9600 ∙ 0.02 = 90 + 192 = 282 Av; ฉัน = (ฉัน ∙ ω) / ω = 282/800 = 0.35 ก.

ในแกนหุ้มเกราะฟลักซ์แม่เหล็กแบ่งออกเป็นสองส่วนซึ่งปิดตามแท่งด้านข้างส่วนตัดขวางคือ S / 2 และความยาวเฉลี่ยของเส้นแม่เหล็กคือ lc เป็นผลให้วงจรแม่เหล็กมีความคล้ายคลึงกับวงจรแม่เหล็กของหม้อแปลงทั่วไปที่มีแกน S ทั่วไปและความยาวของสายไฟ lc

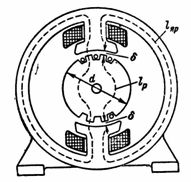
5. ฟลักซ์แม่เหล็กของเครื่อง DC F = 1280000 Mks. วงจรแม่เหล็กประกอบด้วยแอกเหล็กหล่อที่มีความยาวเส้นแม่เหล็กเฉลี่ย lа = 80 ซม. โรเตอร์ประกอบจากแผ่นเหล็กไฟฟ้าที่มีความยาวสนามแม่เหล็กเฉลี่ย lр = 18 ซม. และช่องว่างอากาศสองช่อง δ 0.2 ซม. ในแต่ละช่อง = 8 ∙ 20 ซม.2; ส่วนโรเตอร์และเสา Sр = 12 ∙ 20 cm2... คำนวณ n. หน้า และจำนวนรอบของขดลวดขั้วถ้ากระแสแม่เหล็กสูงสุด (น่าตื่นเต้น) ในนั้นคือ 1 A (รูปที่ 5)

ข้าว. 5.

การเหนี่ยวนำในแอกและเสา Bя = Ф / Sя = 1280000/160 = 8000 G.

แรงดันไฟฟ้าในแอกและเสาตามเส้นโค้งการดึงดูดของเหล็กหล่อที่ Bя = 8000 G เท่ากับ:

H = 2.8 เอ/ซม.

แรงดึงดูดในส่วนของแอก HЯ ∙ la = 2.8 ∙ 80 = 224 Av.

การเหนี่ยวนำในโรเตอร์ เสา และช่องว่างอากาศ Br = Ф / Ср = 1280000/240 = 5333 G.

แรงดันไฟฟ้าในโรเตอร์ที่ทำจากแผ่นเหล็กที่ Br = 5333 Gs Hrp = 0.9 A / cm,

และแรงดันแม่เหล็กของส่วนโรเตอร์ Hр ∙ lр = 0.9 ∙ 18 = 16.2 Av.

แรงดันในช่องว่างอากาศ Hδ = 0.8 ∙ Bδ = 0.8 ∙ 5333 = 4266.4 A / cm.

แรงดันแม่เหล็กในส่วนตัดขวางของช่องว่างอากาศ Hδ ∙ 2 ∙ δ = 4266.4 ∙ 2 ∙ 0.2 = 1706.56 A.

กรอก n c. เท่ากับผลรวมของแรงดันแม่เหล็กในแต่ละส่วน: I ∙ ω = Hя ∙ la + Hр ∙ lр + Hδ ∙ 2 ∙ δ; ฉัน ∙ ω = 224 + 16.2 + 1706.56 = 1946.76 Av.

จำนวนรอบในขดลวดสองขั้ว ω = (I ∙ ω) / I = 1946.76 / 1≈2000