ความต้านทาน การนำไฟฟ้า และวงจรสมมูลของสายไฟ

สายไฟฟ้ามีความต้านทานแบบแอกทีฟและแบบเหนี่ยวนำ และแบบแอคทีฟและแบบคาปาซิทีฟกระจายอย่างสม่ำเสมอตามความยาว

ในการคำนวณทางไฟฟ้าในทางปฏิบัติของเครือข่ายการส่งกำลัง เป็นเรื่องปกติที่จะต้องเปลี่ยนสาย DC ที่กระจายอย่างสม่ำเสมอด้วยค่าคงที่ร่วมกัน: ความต้านทานแบบแอกทีฟ r และอุปนัย x และการนำไฟฟ้าแบบแอกทีฟ g และแบบ capacitive b วงจรสมมูลของเส้นรูปตัวยูที่สอดคล้องกับเงื่อนไขนี้แสดงในรูปที่ 1, ก.

เมื่อคำนวณเครือข่ายการส่งกำลังไฟฟ้าในท้องถิ่นที่มีแรงดันไฟฟ้า 35 kV และต่ำกว่าค่าการนำไฟฟ้า g และ b คุณสามารถเพิกเฉยและใช้วงจรสมมูลที่ง่ายกว่าซึ่งประกอบด้วยความต้านทานแบบแอกทีฟและอินดักทีฟที่เชื่อมต่อแบบอนุกรม (รูปที่ 1, b)

ความต้านทานเชิงเส้นถูกกำหนดโดยสูตร

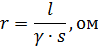
โดยที่ l คือความยาวของเส้นลวด m; s คือส่วนตัดขวางของแกนลวดหรือสายเคเบิล mmg γ คือค่าการนำไฟฟ้าการออกแบบเฉพาะของวัสดุ m / ohm-mm2

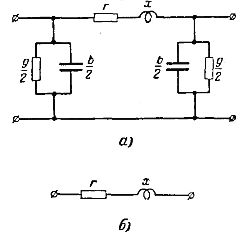
ข้าว. 1. รูปแบบการเปลี่ยนสาย: a — สำหรับเครือข่ายสายส่งไฟฟ้าระดับภูมิภาค; b — สำหรับเครือข่ายสายส่งไฟฟ้าในท้องถิ่น

ค่าเฉลี่ยที่คำนวณได้ของค่าการนำไฟฟ้าเฉพาะที่อุณหภูมิ 20 ° C สำหรับสายแบบแกนเดียวและแบบหลายแกน โดยคำนึงถึงส่วนตัดขวางจริงและความยาวที่เพิ่มขึ้นเมื่อบิดสายแบบมัลติคอร์คือ 53 ม. / โอห์ม ∙ mm2 สำหรับทองแดง, 32 ม./โอห์ม ∙ mm2 สำหรับอะลูมิเนียม

ความต้านทานที่ใช้งานของลวดเหล็กกล้าไม่คงที่ เมื่อกระแสผ่านเส้นลวดเพิ่มขึ้น ผลกระทบของพื้นผิวจะเพิ่มขึ้น ดังนั้นความต้านทานที่ใช้งานของเส้นลวดจึงเพิ่มขึ้น ความต้านทานที่ใช้งานของลวดเหล็กถูกกำหนดโดยเส้นโค้งหรือตารางทดลอง ขึ้นอยู่กับค่าของกระแสที่ไหลผ่าน

เส้นความต้านทานอุปนัย หากสายกระแสสามเฟสถูกสร้างขึ้นด้วยการจัดเรียงใหม่ (การขนย้าย) ของสายไฟจากนั้นที่ความถี่ 50 Hz ความต้านทานการเหนี่ยวนำเฟส 1 กม. ของความยาวสายสามารถกำหนดได้โดยสูตร

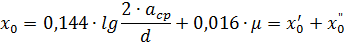
โดยที่: asr คือระยะทางเฉลี่ยทางเรขาคณิตระหว่างแกนของสายไฟ

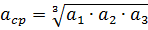
a1, a2 และ a3 คือระยะห่างระหว่างแกนของตัวนำของเฟสต่างๆ d คือเส้นผ่านศูนย์กลางภายนอกของตัวนำตามตาราง GOST สำหรับตัวนำ μ คือการซึมผ่านของแม่เหล็กสัมพัทธ์ของตัวนำโลหะ สำหรับลวดโลหะที่ไม่ใช่เหล็ก μ = 1; x'0 — ความต้านทานการเหนี่ยวนำภายนอกของเส้นเนื่องจากฟลักซ์แม่เหล็กภายนอกตัวนำ x «0 — ความต้านทานอุปนัยภายในของเส้นเนื่องจากฟลักซ์แม่เหล็กที่ปิดอยู่ภายในตัวนำ

ความต้านทานอุปนัยต่อความยาวเส้น l km

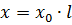
ความต้านทานอุปนัย x0 ของเส้นเหนือศีรษะที่มีตัวนำเป็นโลหะไม่มีธาตุเหล็กอยู่ที่ค่าเฉลี่ย 0.33-0.42 โอห์ม/กม.

เส้นที่มีแรงดันไฟฟ้า 330-500 kV เพื่อลดการสูญเสียของโคโรนัล (ดูด้านล่าง) ไม่ได้ทำด้วยเส้นผ่านศูนย์กลางขนาดใหญ่หนึ่งแกน แต่ใช้ตัวนำเหล็กอลูมิเนียมสองหรือสามตัวต่อเฟสซึ่งอยู่ห่างกันไม่ไกล ในกรณีนี้ ความต้านทานเชิงอุปนัยของเส้นจะลดลงอย่างมาก ในรูป รูปที่ 2 แสดงการใช้งานเฟสที่คล้ายกันบนสาย 500 kV โดยที่ตัวนำสามตัวอยู่ที่จุดยอดของสามเหลี่ยมด้านเท่าที่มีด้านยาว 40 ซม. ตัวนำเฟสได้รับการแก้ไขด้วยแถบแข็งหลายเส้นในส่วนนี้

การใช้สายไฟหลายเส้นต่อเฟสนั้นเทียบเท่ากับการเพิ่มเส้นผ่านศูนย์กลางของเส้นลวด ซึ่งทำให้ความต้านทานอุปนัยของเส้นลดลง หลังสามารถคำนวณได้โดยใช้สูตรที่สองหารเทอมที่สองทางด้านขวาด้วย n และแทนที่ด้วยเส้นผ่านศูนย์กลางภายนอก d ของเส้นลวด เส้นผ่านศูนย์กลางเทียบเท่า de กำหนดโดยสูตร

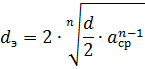
โดยที่ n — จำนวนตัวนำในเฟสหนึ่งของสาย acp — ระยะห่างเฉลี่ยทางเรขาคณิตระหว่างตัวนำของเฟสเดียว

ด้วยสายไฟสองเส้นต่อเฟสความต้านทานเชิงอุปนัยของเส้นจะลดลงประมาณ 15-20% และด้วยสายไฟสามเส้น - 25-30%

ส่วนตัดขวางทั้งหมดของตัวนำเฟสเท่ากับส่วนตัดขวางของการออกแบบที่ต้องการ ส่วนหลังจะถูกแบ่งออกเป็นสองหรือสามตัวนำ ซึ่งเป็นเหตุผลว่าทำไมเส้นดังกล่าวจึงเรียกว่าเส้นแยกตัวนำตามอัตภาพ

ลวดเหล็กกล้ามีค่า x0 มาก เนื่องจาก การซึมผ่านของแม่เหล็ก กลายเป็นมากกว่าหนึ่งและพจน์ที่สองของสูตรที่สองคือตัวชี้ขาด นั่นคือ ความต้านทานภายในอุปนัย x «0

ข้าว. 2. 500 ตร.ม. เฟสเดียวสามสายแยกพวงมาลัยแขวน

เนื่องจากการซึมผ่านของแม่เหล็กของเหล็กขึ้นอยู่กับค่าของกระแสที่ไหลผ่านลวดจึงค่อนข้างยากที่จะกำหนด x «0 จากลวดเหล็ก ดังนั้นในการคำนวณเชิงปฏิบัติ x» 0 ของเส้นลวดเหล็กจะถูกกำหนดจากเส้นโค้งหรือตารางที่ได้จากการทดลอง

ความต้านทานแบบเหนี่ยวนำของสายเคเบิลแบบสามแกนสามารถยึดตามค่าเฉลี่ยต่อไปนี้:

• สำหรับสายไฟสามเส้น 35 kV — 0.12 โอห์ม/กม

• สำหรับสายไฟสามเส้น 3-10 kv-0.07-0.03 โอห์ม/กม.

• สำหรับสายเคเบิลสามสายสูงถึง 1 kV-0.06-0.07 โอห์ม/กม.

เส้นนำไฟฟ้าแบบแอคทีฟถูกกำหนดโดยการสูญเสียพลังงานที่ใช้งานในไดอิเล็กตริก

ในสายไฟเหนือศีรษะของแรงดันไฟฟ้าทั้งหมด การสูญเสียผ่านฉนวนมีเพียงเล็กน้อยแม้ในบริเวณที่มีอากาศเสียสูง ดังนั้นจึงไม่นำมาพิจารณา

ในสายไฟเหนือศีรษะที่มีแรงดันไฟฟ้า 110 kV ขึ้นไป ภายใต้เงื่อนไขบางประการ โคโรนาจะปรากฏบนสายไฟ เนื่องจากการไอออไนซ์ที่รุนแรงของอากาศรอบๆ สายไฟ และมาพร้อมกับแสงสีม่วงและเสียงแตกที่มีลักษณะเฉพาะ เม็ดมะยมมีความแข็งเป็นพิเศษในสภาพอากาศที่เปียกชื้น วิธีที่รุนแรงที่สุดในการลดการสูญเสียพลังงานให้กับโคโรนาคือการเพิ่มขนาดเส้นผ่านศูนย์กลางของตัวนำ เนื่องจากเมื่อค่าหลังเพิ่มขึ้น ความแรงของสนามไฟฟ้า และดังนั้น ไอออนไนซ์ของอากาศใกล้กับตัวนำจึงลดลง

สำหรับเส้น 110 kV เส้นผ่านศูนย์กลางของตัวนำจากสภาวะโคโรนาควรมีอย่างน้อย 10-11 มม. (ตัวนำ AC-50 และ M-70) สำหรับเส้น 154 kV - อย่างน้อย 14 มม. (ตัวนำ AC-95) และ สำหรับสาย 220 kV — ไม่น้อยกว่า 22 มม. (ตัวนำ AC -240)

การสูญเสียพลังงานที่ใช้งานสำหรับโคโรนาในตัวนำขนาด 110-220 kV เหนือศีรษะของเส้นผ่านศูนย์กลางตัวนำที่ระบุและมีขนาดใหญ่นั้นไม่มีนัยสำคัญ (หลายสิบกิโลวัตต์ต่อความยาวเส้น 1 กม.) ดังนั้นจึงไม่นำมาพิจารณาในการคำนวณ

ในสาย 330 และ 500 kV จะใช้ตัวนำสองหรือสามตัวต่อเฟสซึ่งดังที่ได้กล่าวไว้ก่อนหน้านี้เทียบเท่ากับการเพิ่มเส้นผ่านศูนย์กลางของตัวนำซึ่งเป็นผลมาจากความแรงของสนามไฟฟ้าใกล้กับตัวนำมีนัยสำคัญ ลดลงและตัวนำสึกกร่อนเล็กน้อย

ในสายเคเบิลขนาด 35 kV และต่ำกว่า การสูญเสียพลังงานในไดอิเล็กตริกจะมีเพียงเล็กน้อยและไม่ได้นำมาพิจารณาด้วย ในสายเคเบิลที่มีแรงดันไฟฟ้า 110 kV ขึ้นไป การสูญเสียไดอิเล็กตริกจะอยู่ที่หลายกิโลวัตต์ต่อความยาว 1 กม.

การนำประจุของสายเนื่องจากความจุระหว่างตัวนำและระหว่างตัวนำกับพื้น

ด้วยความแม่นยำที่เพียงพอสำหรับการคำนวณเชิงปฏิบัติ ค่าการนำไฟฟ้าแบบคาปาซิทีฟของสายโอเวอร์เฮดไลน์สามเฟสสามารถกำหนดได้จากสูตร

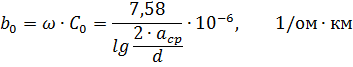
โดยที่ C0 คือความสามารถในการทำงานของสาย ω — ความถี่เชิงมุมของกระแสสลับ acp และ d — ดูด้านบน

ในกรณีนี้ จะไม่คำนึงถึงการนำไฟฟ้าของดินและความลึกของกระแสไฟฟ้าที่ไหลกลับลงสู่พื้นดิน และสันนิษฐานว่ามีการจัดเรียงตัวนำใหม่ตลอดแนว

สำหรับสายเคเบิล ความสามารถในการทำงานจะถูกกำหนดตามข้อมูลจากโรงงาน

การนำเชิงเส้น l km

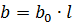
การปรากฏตัวของความจุในสายทำให้กระแส capacitive ไหล กระแสตัวเก็บประจุอยู่ข้างหน้า 90° ของแรงดันเฟสที่สอดคล้องกัน

ในเส้นจริงที่มีกระแสประจุคงที่กระจายอย่างสม่ำเสมอตลอดความยาว กระแสประจุไฟฟ้าจะไม่สม่ำเสมอตลอดความยาวของเส้น เนื่องจากแรงดันตกคร่อมเส้นมีขนาดไม่คงที่

กระแสตัวเก็บประจุที่จุดเริ่มต้นของบรรทัดรับแรงดันไฟฟ้ากระแสตรง

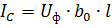
โดยที่ Uph คือแรงดันเฟสของเส้น

สายไฟ Capacitive (พลังงานที่สร้างขึ้นโดยสาย)

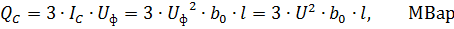
โดยที่ U คือแรงดันเฟสต่อเฟส, ตร.ม.

จากสูตรที่สามพบว่าค่าการนำไฟฟ้าแบบ capacitive ของเส้นขึ้นอยู่กับระยะห่างระหว่างตัวนำและเส้นผ่านศูนย์กลางของตัวนำเพียงเล็กน้อย พลังงานที่สร้างขึ้นโดยสายนั้นขึ้นอยู่กับแรงดันไฟฟ้าของสายเป็นอย่างมาก สำหรับสายเหนือศีรษะ 35 kV และต่ำกว่านั้นมีขนาดเล็กมาก สำหรับสาย 110 kV ที่มีความยาว 100 กม. Qc≈3 Mvar สำหรับสาย 220 kV ที่มีความยาว 100 กม. Qc≈13 Mvar การแยกสายจะเพิ่มความจุของสาย

กระแสความจุของเครือข่ายเคเบิลจะนำมาพิจารณาที่แรงดันไฟฟ้า 20 kV ขึ้นไปเท่านั้น