การสูญเสียและแรงดันไฟฟ้าตก - อะไรคือความแตกต่าง
 ในชีวิตมนุษย์ทั่วไป คำว่า "สูญเสีย" และ "ตก" ใช้เพื่อแสดงถึงข้อเท็จจริงของความสำเร็จบางอย่างที่ลดลง แต่หมายถึงคุณค่าที่แตกต่างกัน
ในชีวิตมนุษย์ทั่วไป คำว่า "สูญเสีย" และ "ตก" ใช้เพื่อแสดงถึงข้อเท็จจริงของความสำเร็จบางอย่างที่ลดลง แต่หมายถึงคุณค่าที่แตกต่างกัน
ในกรณีนี้ «การสูญเสีย» หมายถึงการสูญเสียชิ้นส่วน ความเสียหาย การลดขนาดของระดับที่สำเร็จก่อนหน้านี้ การสูญเสียเป็นสิ่งที่ไม่พึงปรารถนา แต่คุณสามารถยอมรับได้
คำว่า "ตก" เป็นที่เข้าใจกันว่าเป็นอันตรายร้ายแรงที่เกี่ยวข้องกับการลิดรอนสิทธิโดยสิ้นเชิง ดังนั้น แม้แต่การสูญเสียที่เกิดขึ้นเป็นครั้งคราว (เช่น พอร์ตโฟลิโอ) เมื่อเวลาผ่านไปก็สามารถนำไปสู่การลดลงได้ (เช่น ระดับของอายุการใช้งานทางวัตถุ)
ในเรื่องนี้เราจะพิจารณาคำถามนี้เกี่ยวกับแรงดันไฟฟ้าของเครือข่ายไฟฟ้า
การสูญเสียและแรงดันตกเกิดขึ้นได้อย่างไร
ไฟฟ้าถูกส่งไปในระยะทางไกลโดยสายเหนือศีรษะจากสถานีย่อยหนึ่งไปยังอีกสถานีหนึ่ง
เส้นค่าใช้จ่ายได้รับการออกแบบเพื่อส่งพลังงานที่อนุญาตและทำจากลวดโลหะของวัสดุและส่วนเฉพาะ พวกเขาสร้างโหลดตัวต้านทานที่มีค่าความต้านทาน R และโหลดปฏิกิริยา X
ด้านรับมันยืนอยู่ หม้อแปลงการแปลงไฟฟ้าขดลวดมีความต้านทานแบบเหนี่ยวนำ XL ที่ทำงานอยู่และเด่นชัด ด้านทุติยภูมิของหม้อแปลงจะลดแรงดันไฟฟ้าลงและส่งต่อไปยังผู้บริโภค ซึ่งโหลดจะแสดงด้วยค่า Z และมีลักษณะใช้งาน ตัวเก็บประจุ และอุปนัย นอกจากนี้ยังส่งผลต่อพารามิเตอร์ทางไฟฟ้าของเครือข่าย
แรงดันไฟฟ้าที่ใช้กับสายไฟของส่วนรองรับของสายเหนือศีรษะซึ่งอยู่ใกล้กับสถานีส่งกำลังไฟฟ้ามากที่สุด เอาชนะความต้านทานปฏิกิริยาและแอคทีฟของวงจรในแต่ละเฟสและสร้างกระแสในนั้น ซึ่งเวกเตอร์นั้นเบี่ยงเบนไปจากเวกเตอร์ของ แรงดันไฟฟ้าที่ใช้โดยมุม φ
ลักษณะของการกระจายแรงดันและการไหลของกระแสตามแนวเส้นสำหรับโหมดโหลดแบบสมมาตรแสดงในภาพถ่าย
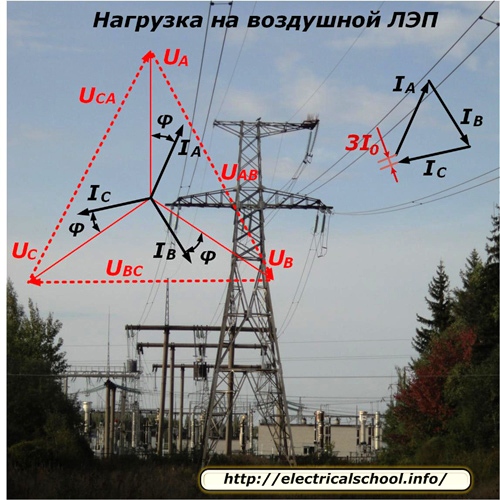
เนื่องจากแต่ละเฟสของสายป้อนผู้บริโภคในจำนวนที่แตกต่างกันซึ่งถูกตัดการเชื่อมต่อแบบสุ่มหรือเชื่อมต่อกับงานด้วย จึงเป็นเรื่องยากมากในทางเทคนิคที่จะสร้างสมดุลระหว่างโหลดเฟสอย่างสมบูรณ์แบบ มีความไม่สมดุลอยู่เสมอ ซึ่งถูกกำหนดโดยการเพิ่มเวกเตอร์ของกระแสเฟสและเขียนเป็น 3I0 ในการคำนวณส่วนใหญ่จะละเว้น
พลังงานที่ใช้โดยสถานีย่อยที่ส่งสัญญาณนั้นถูกใช้ไปบางส่วนเพื่อเอาชนะแนวต้านของสายและไปถึงด้านรับโดยมีการเปลี่ยนแปลงเพียงเล็กน้อย เศษส่วนนี้มีลักษณะเฉพาะคือการสูญเสียและแรงดันตก ซึ่งเวกเตอร์นั้นจะลดลงเล็กน้อยในแอมพลิจูดและถูกเลื่อนไปตามมุมในแต่ละเฟส
วิธีคำนวณความสูญเสียและแรงดันตก
เพื่อให้เข้าใจกระบวนการที่เกิดขึ้นระหว่างการส่งกระแสไฟฟ้า รูปแบบเวกเตอร์จะสะดวกสำหรับการแสดงลักษณะสำคัญ วิธีการคำนวณทางคณิตศาสตร์ต่าง ๆ ก็ใช้วิธีนี้เช่นกัน
เพื่อให้การคำนวณง่ายขึ้น ระบบสามเฟส มันถูกแสดงด้วยวงจรสมมูลเฟสเดียวสามวงจร วิธีนี้ใช้ได้ดีกับการโหลดแบบสมมาตร และช่วยให้คุณวิเคราะห์กระบวนการต่างๆ เมื่อเกิดการเสียได้
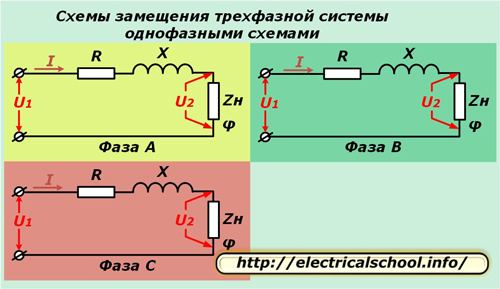
ในไดอะแกรมด้านบน R ที่ใช้งานอยู่และรีแอกแตนซ์ X ของตัวนำแต่ละตัวของเส้นจะเชื่อมต่อแบบอนุกรมกับ Zn ที่มีความต้านทานโหลดเชิงซ้อนที่แสดงโดยมุม φ
นอกจากนี้ยังทำการคำนวณการสูญเสียแรงดันและแรงดันตกในเฟสเดียว ในการทำเช่นนี้คุณต้องระบุข้อมูล เพื่อจุดประสงค์นี้ มีการเลือกสถานีย่อยที่รับพลังงานซึ่งต้องกำหนดโหลดที่อนุญาตแล้ว
ค่าแรงดันไฟฟ้าของระบบไฟฟ้าแรงสูงใด ๆ ระบุไว้แล้วในหนังสืออ้างอิง และความต้านทานของสายไฟถูกกำหนดโดยความยาว ส่วนตัดขวาง วัสดุและการกำหนดค่าของเครือข่าย กระแสสูงสุดในวงจรถูกกำหนดและจำกัดโดยคุณสมบัติของสายไฟ
ดังนั้นเพื่อเริ่มการคำนวณ เรามี: U2, R, X, Z, I, φ
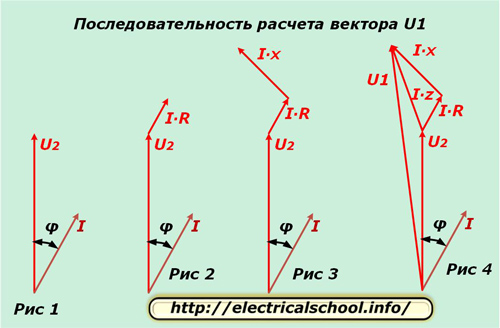
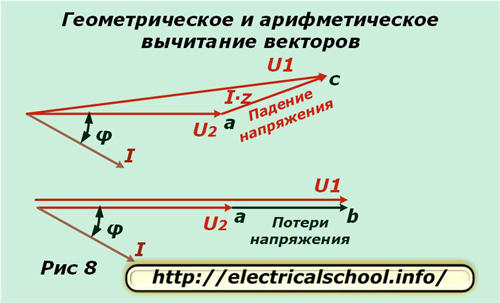
เราใช้เฟสเดียวเช่น «A» และแยกเวกเตอร์ U2 และ I ออกจากระนาบเชิงซ้อนซึ่งแทนที่ด้วยมุม φ ดังแสดงในรูปที่ 1 ความต่างศักย์ในความต้านทานที่ใช้งานของตัวนำเกิดขึ้นพร้อมกันในทิศทาง ด้วยกระแสและขนาดถูกกำหนดจากนิพจน์ I ∙ R เราเลื่อนเวกเตอร์นี้ออกจากจุดสิ้นสุดของ U2 (รูปที่ 2)
ความต่างศักย์ในรีแอกแตนซ์ของตัวนำแตกต่างจากทิศทางของกระแสด้วยมุม φ1 และคำนวณจากผลิตภัณฑ์ I ∙ X เราเลื่อนมันออกจากเวกเตอร์ I ∙ R (รูปที่ 3)
คำเตือน: สำหรับทิศทางบวกของการหมุนของเวกเตอร์ในระนาบเชิงซ้อน การเคลื่อนไหวทวนเข็มนาฬิกาจะถูกนำมาใช้ กระแสที่ไหลผ่านโหลดอุปนัยจะหน่วงแรงดันไฟฟ้าที่ใช้เป็นมุม
รูปที่ 4 แสดงการพล็อตเวกเตอร์ความต่างศักย์บนความต้านทานของเส้นลวดทั้งหมด I ∙ Z และแรงดันไฟฟ้าที่อินพุตของวงจร U1
ตอนนี้คุณสามารถเปรียบเทียบเวกเตอร์อินพุตกับวงจรสมมูลและข้ามโหลดได้ ในการทำเช่นนี้ให้วางไดอะแกรมผลลัพธ์ในแนวนอน (รูปที่ 5) แล้ววาดส่วนโค้งจากจุดเริ่มต้นด้วยรัศมีของโมดูล U1 จนกว่าจะตัดกับทิศทางของเวกเตอร์ U2 (รูปที่ 6)
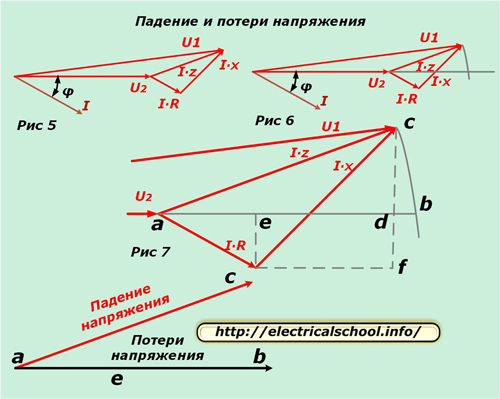
รูปที่ 7 แสดงการขยายรูปสามเหลี่ยมเพื่อความชัดเจนยิ่งขึ้นและการวาดเส้นเสริมซึ่งระบุจุดตัดที่มีลักษณะเฉพาะด้วยตัวอักษร
ที่ด้านล่างของภาพ จะเห็นว่าเวกเตอร์ที่เป็นผลลัพธ์เรียกว่า แรงดันตก และ ab เรียกว่า การสูญเสีย มีขนาดและทิศทางต่างกัน หากเรากลับไปที่มาตราส่วนเดิม เราจะเห็นว่า ac ได้มาจากการลบทางเรขาคณิตของเวกเตอร์ (U2 จาก U1) และ ab เป็นเลขคณิต กระบวนการนี้แสดงในรูปภาพด้านล่าง (รูปที่ 8)
ที่มาของสูตรสำหรับการคำนวณการสูญเสียแรงดันไฟฟ้า
ทีนี้ลองกลับไปที่รูปที่ 7 และสังเกตว่าส่วน bd นั้นเล็กมาก ด้วยเหตุนี้จึงถูกละเลยในการคำนวณและคำนวณการสูญเสียแรงดันไฟฟ้าจากโฆษณาความยาวเซ็กเมนต์ ประกอบด้วยสองส่วนของเส้นตรง ae และ ed
เนื่องจาก ae = I ∙ R ∙ cosφ และ ed = I ∙ x ∙ sinφ ดังนั้น การสูญเสียแรงดันไฟฟ้าสำหรับหนึ่งเฟสสามารถคำนวณได้จากสูตร:
∆อัพ = I ∙ R ∙ cosφ + I ∙ x ∙ sinφ
หากเราคิดว่าโหลดมีความสมมาตรในทุกเฟส (ละเลย 3I0 อย่างมีเงื่อนไข) เราสามารถใช้วิธีทางคณิตศาสตร์เพื่อคำนวณการสูญเสียแรงดันไฟฟ้าในสาย
∆Ul = √3I ∙ (R ∙ cosφ + x ∙ บาปφ)
หากทางด้านขวาของสูตรนี้คูณและหารด้วยแรงดันไฟฟ้าเครือข่าย Un เราจะได้สูตรที่ช่วยให้เราคำนวณ p ของการสูญเสียแรงดันไฟฟ้าผ่านแหล่งจ่ายไฟ
∆Ul = (P ∙ r + Q ∙ x) / Un
ค่าของพลังงาน P ที่ใช้งานและปฏิกิริยา Q สามารถนำมาจากการอ่านมิเตอร์วัดได้
ดังนั้น การสูญเสียแรงดันไฟฟ้าในวงจรไฟฟ้าจึงขึ้นอยู่กับ:
-
แอกทีฟและรีแอกแตนซ์ของวงจร
-
ส่วนประกอบของกำลังไฟฟ้าที่ใช้
-
ขนาดของแรงดันไฟฟ้าที่ใช้
ที่มาของสูตรสำหรับการคำนวณองค์ประกอบตามขวางของแรงดันตก
กลับไปที่รูปที่ 7 ค่าของเวกเตอร์ ac สามารถแสดงด้วยด้านตรงข้ามมุมฉากของสามเหลี่ยมมุมฉาก acd เราได้คำนวณฐานโฆษณาแล้ว ให้เรากำหนดองค์ประกอบตามขวาง cd
รูปแสดงว่า cd = cf-df
df = ce = ฉัน ∙ R ∙ บาป φ
cf = I ∙ x ∙ cos φ
cd = I ∙ x ∙ cosφ-I ∙ R ∙ sinφ
เราใช้แบบจำลองที่ได้รับ เราทำการแปลงทางคณิตศาสตร์ขนาดเล็กและรับส่วนประกอบตามขวางของแรงดันตก
δU = √3I ∙ (x ∙ cosφ-r ∙ sinφ) = (P ∙ x-Q ∙ r) / Un
การกำหนดสูตรการคำนวณแรงดันไฟฟ้า U1 ที่จุดเริ่มต้นของสายไฟ
เมื่อทราบค่าของแรงดันที่ปลายเส้น U2 การสูญเสีย ∆Ul และองค์ประกอบตามขวางของหยด δU เราสามารถคำนวณค่าของเวกเตอร์ U1 ได้ด้วยทฤษฎีบทพีทาโกรัส ในรูปแบบขยายมีรูปแบบดังต่อไปนี้
U1 = √ [(U2 + (Pr + Qx) / Un)2+ ((Px-Qr) / Un)2].
ใช้งานได้จริง
การคำนวณการสูญเสียแรงดันไฟฟ้าดำเนินการโดยวิศวกรในขั้นตอนของการสร้างโครงการวงจรไฟฟ้าเพื่อเลือกการกำหนดค่าเครือข่ายและองค์ประกอบที่เหมาะสมที่สุด
ในระหว่างการทำงานของการติดตั้งระบบไฟฟ้าหากจำเป็นสามารถดำเนินการวัดเวกเตอร์แรงดันไฟฟ้าพร้อมกันที่ปลายเส้นเป็นระยะและสามารถเปรียบเทียบผลลัพธ์ที่ได้จากวิธีการคำนวณอย่างง่าย ๆ วิธีนี้เหมาะสำหรับอุปกรณ์ที่เพิ่มขึ้น เนื่องจากต้องการความแม่นยำในการทำงานสูง
การสูญเสียแรงดันไฟฟ้าในวงจรทุติยภูมิ
ตัวอย่างคือวงจรทุติยภูมิของหม้อแปลงวัดแรงดัน ซึ่งบางครั้งมีความยาวหลายร้อยเมตรและถูกส่งโดยสายไฟพิเศษที่มีหน้าตัดเพิ่มขึ้น
คุณสมบัติทางไฟฟ้าของสายเคเบิลดังกล่าวขึ้นอยู่กับข้อกำหนดที่เพิ่มขึ้นสำหรับคุณภาพของการส่งแรงดันไฟฟ้า
การป้องกันอุปกรณ์ไฟฟ้าสมัยใหม่ต้องการการทำงานของระบบการวัดที่มีตัวบ่งชี้มาตรวิทยาสูงและระดับความแม่นยำ 0.5 หรือ 0.2 ดังนั้นจึงต้องตรวจสอบและคำนึงถึงการสูญเสียของแรงดันไฟฟ้าที่ใช้กับพวกมัน มิฉะนั้นข้อผิดพลาดที่พวกเขานำมาใช้ในการทำงานของอุปกรณ์อาจส่งผลต่อลักษณะการทำงานทั้งหมดอย่างมีนัยสำคัญ
การสูญเสียแรงดันไฟฟ้าในสายเคเบิลยาว
คุณลักษณะของการออกแบบสายเคเบิลยาวคือมีความต้านทาน capacitive เนื่องจากการจัดเรียงแกนตัวนำที่ค่อนข้างชิดและชั้นฉนวนบาง ๆ ระหว่างกัน มันยังเบี่ยงเบนเวกเตอร์ปัจจุบันที่ผ่านสายเคเบิลและเปลี่ยนขนาดของมัน
ต้องคำนึงถึงผลกระทบของแรงดันตกบนความต้านทานตัวเก็บประจุในการคำนวณเพื่อเปลี่ยนค่า I ∙ z มิฉะนั้น เทคโนโลยีที่อธิบายข้างต้นจะไม่เปลี่ยนแปลง
บทความนี้แสดงตัวอย่างการสูญเสียและแรงดันไฟฟ้าตกบนสายไฟและสายเคเบิลเหนือศีรษะ อย่างไรก็ตาม พบได้ในผู้ใช้ไฟฟ้าทั้งหมด รวมถึงมอเตอร์ไฟฟ้า หม้อแปลงไฟฟ้า ตัวเหนี่ยวนำ ตัวเก็บประจุไฟฟ้า และอุปกรณ์อื่นๆ
ปริมาณการสูญเสียแรงดันไฟฟ้าสำหรับอุปกรณ์ไฟฟ้าแต่ละประเภทได้รับการควบคุมตามกฎหมายในแง่ของสภาพการใช้งาน และหลักการในการพิจารณาในวงจรไฟฟ้าทั้งหมดจะเหมือนกัน

