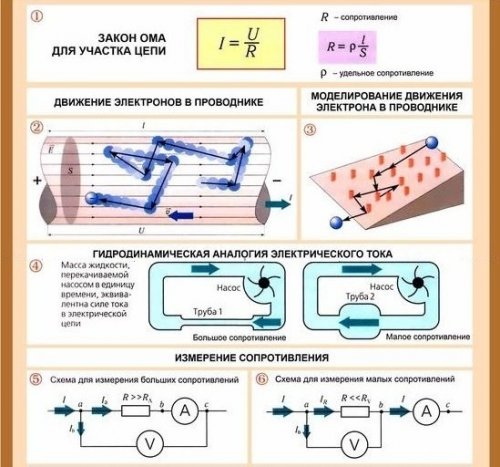
กฎของโอห์มสำหรับส่วนของวงจร

กฎพื้นฐานของวิศวกรรมไฟฟ้าที่คุณสามารถใช้เพื่อศึกษาและคำนวณวงจรไฟฟ้าคือกฎของโอห์ม ซึ่งสร้างความสัมพันธ์ระหว่างกระแส แรงดัน และความต้านทาน จำเป็นต้องเข้าใจสาระสำคัญอย่างชัดเจนและสามารถนำไปใช้ได้อย่างถูกต้องในการแก้ปัญหาในทางปฏิบัติ ข้อผิดพลาดมักเกิดขึ้นในวิศวกรรมไฟฟ้าเนื่องจากไม่สามารถใช้กฎของโอห์มได้อย่างถูกต้อง

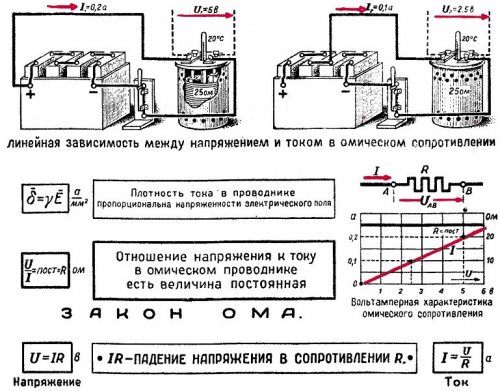
กฎของโอห์มสำหรับส่วนของสถานะวงจร: กระแสเป็นสัดส่วนโดยตรงกับแรงดันและแปรผกผันกับความต้านทาน

ถ้าแรงดันไฟฟ้าที่กระทำในวงจรไฟฟ้าเพิ่มขึ้นหลายเท่า กระแสในวงจรนั้นจะเพิ่มขึ้นตามจำนวนที่เท่ากัน และถ้าคุณเพิ่มความต้านทานของวงจรหลาย ๆ ครั้ง กระแสจะลดลงตามจำนวนที่เท่ากัน ในทำนองเดียวกัน การไหลของน้ำในท่อยิ่งมาก แรงดันยิ่งแรง และความต้านทานของท่อต่อการเคลื่อนที่ของน้ำก็จะยิ่งน้อยลง

ในรูปแบบที่นิยม กฎนี้สามารถกำหนดได้ดังนี้: ยิ่งแรงดันไฟฟ้าสูงสำหรับความต้านทานเดียวกัน กระแสไฟฟ้าก็จะยิ่งสูงขึ้น และในเวลาเดียวกัน ความต้านทานสำหรับแรงดันไฟฟ้าเดียวกันก็จะยิ่งสูงขึ้น แอมแปร์ก็จะยิ่งต่ำลง

ในการแสดงกฎของโอห์มทางคณิตศาสตร์ด้วยวิธีที่ง่ายที่สุดที่เป็นไปได้ ความต้านทานของสายไฟที่มีกระแส 1 A ที่แรงดัน 1 V จะถือเป็น 1 โอห์ม

กระแสเป็นแอมแปร์สามารถกำหนดได้เสมอโดยการหารแรงดันเป็นโวลต์ด้วยความต้านทานเป็นโอห์ม ดังนั้นกฎของโอห์มสำหรับส่วนของวงจรจึงเขียนด้วยสูตรต่อไปนี้:

ฉัน = U / R

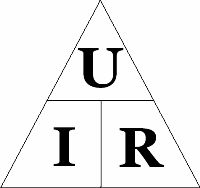
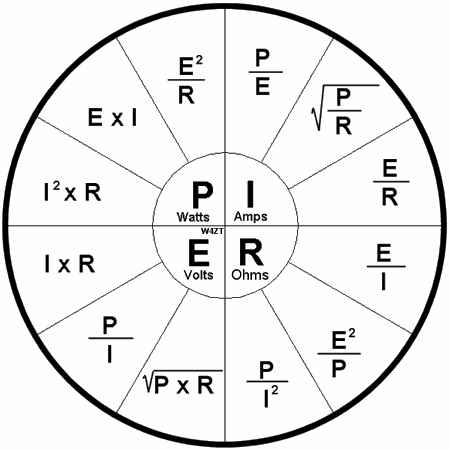
สามเหลี่ยมวิเศษ

ส่วนหรือส่วนประกอบใดๆ ของวงจรไฟฟ้าสามารถจำแนกลักษณะได้ 3 ลักษณะ คือ กระแส แรงดัน และความต้านทาน

วิธีใช้สามเหลี่ยมของโอห์ม: เราปิดค่าที่ต้องการ — สัญลักษณ์อีกสองตัวจะให้สูตรสำหรับการคำนวณ โดยวิธีการที่มีเพียงสูตรเดียวจากรูปสามเหลี่ยมที่เรียกว่ากฎของโอห์ม ซึ่งเป็นสูตรที่สะท้อนถึงการพึ่งพากระแสกับแรงดันและความต้านทาน อีกสองสูตรแม้ว่าจะเป็นผลของมัน แต่ก็ไม่สมเหตุสมผล

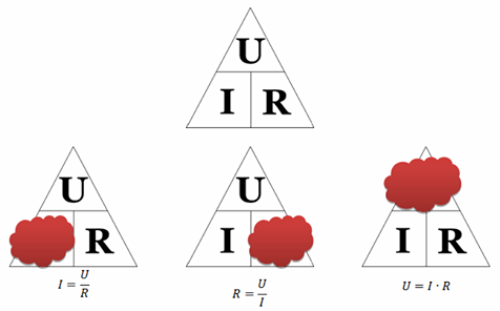
การคำนวณโดยใช้กฎของโอห์มสำหรับส่วนของวงจรจะถูกต้องเมื่อแรงดันไฟฟ้ามีหน่วยเป็นโวลต์ ความต้านทานมีหน่วยเป็นโอห์ม และกระแสไฟฟ้ามีหน่วยเป็นแอมแปร์ หากใช้ปริมาณเหล่านี้หลายหน่วย (เช่น มิลลิแอมป์ มิลลิโวลต์ เมกะโอห์ม ฯลฯ) จะต้องแปลงเป็นแอมแปร์ โวลต์ และโอห์มตามลำดับ เพื่อเน้นสิ่งนี้ บางครั้งสูตรกฎของโอห์มสำหรับส่วนของวงจรจะเขียนดังนี้:

แอมป์ = โวลต์/โอห์ม

คุณยังสามารถคำนวณกระแสเป็นมิลลิแอมป์และไมโครแอมป์ได้ ในขณะที่แรงดันไฟฟ้าควรแสดงเป็นโวลต์และความต้านทานเป็นกิโลโอห์มและเมกะโอห์ม ตามลำดับ

บทความอื่น ๆ เกี่ยวกับไฟฟ้าด้วยวิธีที่ง่ายและราคาไม่แพง:

แรงดัน กระแส และความต้านทานคืออะไร: ใช้อย่างไรในทางปฏิบัติ

ความต้านทานขึ้นอยู่กับอุณหภูมิ

แหล่งที่มาของ EMF และปัจจุบัน: ลักษณะสำคัญและความแตกต่าง

แหล่งจ่ายไฟฟ้าคืออะไร?

สนามไฟฟ้าและสนามแม่เหล็ก—อะไรคือความแตกต่าง?

กฎของโอห์มใช้ได้กับทุกส่วนของวงจร หากจำเป็นต้องกำหนดกระแสในส่วนที่กำหนดของวงจร จำเป็นต้องแบ่งแรงดันที่ทำหน้าที่ในส่วนนี้ (รูปที่ 1) ด้วยความต้านทานของส่วนนี้

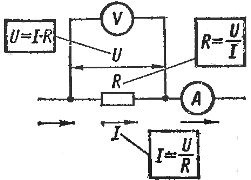
รูปที่ 1 การใช้กฎของโอห์มในส่วนของวงจร

ขอยกตัวอย่างการคำนวณกระแสตามกฎของโอห์ม... ให้กำหนดกระแสในหลอดไฟที่มีความต้านทาน 2.5 โอห์ม หากแรงดันไฟฟ้าที่ใช้กับหลอดไฟคือ 5 V หาร 5 V ด้วย 2.5 โอห์ม เราจะได้ค่ากระแสเท่ากับ 2 A ในตัวอย่างที่สอง เรากำหนดกระแสที่จะไหลภายใต้อิทธิพลของแรงดันไฟฟ้า 500 V ในวงจรที่มีความต้านทาน 0.5 MΩ ในการทำเช่นนี้เราจะแสดงความต้านทานเป็นโอห์ม หาร 500 V ด้วย 500,000 โอห์ม เราพบกระแสในวงจรซึ่งเท่ากับ 0.001 A หรือ 1 mA

บ่อยครั้งที่ทราบกระแสและความต้านทานแรงดันไฟฟ้าจะถูกกำหนดโดยใช้กฎของโอห์ม ลองเขียนสูตรเพื่อกำหนดแรงดันไฟฟ้า

ยู = ไออาร์

สูตรนี้แสดงให้เห็นว่าแรงดันไฟฟ้าที่ปลายส่วนที่กำหนดของวงจรเป็นสัดส่วนโดยตรงกับกระแสและความต้านทาน... ความหมายของการพึ่งพาอาศัยกันนี้เข้าใจได้ไม่ยากหากความต้านทานของส่วนวงจรไม่เปลี่ยนแปลง กระแสจะเพิ่มขึ้นได้โดยการเพิ่มแรงดันเท่านั้น ซึ่งหมายความว่าที่ความต้านทานคงที่ กระแสไฟฟ้าที่มากขึ้นจะสอดคล้องกับแรงดันไฟฟ้าที่มากขึ้น หากจำเป็นต้องได้รับกระแสเดียวกันที่ความต้านทานต่างกัน ความต้านทานที่สูงขึ้นจะต้องมีแรงดันไฟฟ้าที่สูงขึ้นตามลำดับ

แรงดันไฟฟ้าข้ามส่วนของวงจรมักถูกเรียกว่าแรงดันตก... สิ่งนี้มักนำไปสู่ความเข้าใจผิด หลายคนคิดว่าแรงดันไฟฟ้าตกคือการสูญเสียแรงดันไฟฟ้าโดยไม่จำเป็น ในความเป็นจริง แนวคิดของแรงดันและแรงดันตกมีค่าเท่ากัน การสูญเสียและแรงดันตก—อะไรคือความแตกต่าง?

แรงดันตกคร่อมคือความต่างศักย์ที่ลดลงอย่างค่อยเป็นค่อยไปทั่วทั้งวงจรที่มีกระแสไฟฟ้าเนื่องจากวงจรมีความต้านทานที่ทำงานอยู่ ตามกฎของโอห์ม แรงดันตกในแต่ละส่วนของวงจร U เท่ากับผลคูณของความต้านทานของส่วนนี้ของวงจร R โดยกระแสในนั้น I เช่น ยู — RI ดังนั้น ยิ่งส่วนใดของวงจรมีความต้านทานมากเท่าใด แรงดันตกคร่อมในส่วนนั้นของวงจรก็จะยิ่งมากขึ้นเท่านั้น

การคำนวณแรงดันตามกฎของโอห์มสามารถแสดงได้ในตัวอย่างต่อไปนี้ ปล่อยให้กระแส 5 mA ผ่านส่วนของวงจรที่มีความต้านทาน 10 kOhm และจำเป็นต้องกำหนดแรงดันไฟฟ้าในส่วนนี้

โดยการคูณ A = 0.005 A ที่ R — 10,000 Ω เราจะได้แรงดันไฟฟ้าเท่ากับ 50 V สามารถรับผลลัพธ์เดียวกันได้โดยการคูณ 5 mA ด้วย 10 kΩ: U = 50 in

ในอุปกรณ์อิเล็กทรอนิกส์ กระแสมักจะแสดงเป็นมิลลิแอมป์และความต้านทานเป็นกิโลโอห์มดังนั้นจึงสะดวกที่จะใช้หน่วยการวัดเหล่านี้ในการคำนวณตามกฎหมายของโอห์ม

กฎของโอห์มยังคำนวณความต้านทานหากทราบแรงดันและกระแส สูตรสำหรับกรณีนี้เขียนดังนี้: R = U / I

ความต้านทานคืออัตราส่วนของแรงดันต่อกระแสเสมอ ถ้าแรงดันไฟฟ้าเพิ่มขึ้นหรือลดลงหลายครั้ง กระแสไฟฟ้าจะเพิ่มขึ้นหรือลดลงในจำนวนครั้งเท่ากัน อัตราส่วนแรงดันกระแสเท่ากับความต้านทานยังคงไม่เปลี่ยนแปลง

ไม่ควรเข้าใจสูตรสำหรับการกำหนดความต้านทานว่าความต้านทานของตัวนำที่กำหนดนั้นขึ้นอยู่กับกระแสและแรงดัน เป็นที่ทราบกันว่าขึ้นอยู่กับความยาว พื้นที่หน้าตัด และวัสดุของเส้นลวด ในลักษณะที่ปรากฏสูตรสำหรับการกำหนดความต้านทานคล้ายกับสูตรสำหรับการคำนวณกระแส แต่มีความแตกต่างพื้นฐานระหว่างพวกเขา

กระแสในส่วนที่กำหนดของวงจรขึ้นอยู่กับแรงดันและความต้านทานและการเปลี่ยนแปลงเมื่อมีการเปลี่ยนแปลง และความต้านทานของวงจรส่วนนี้เป็นค่าคงที่ที่ไม่ขึ้นอยู่กับการเปลี่ยนแปลงของแรงดันและกระแส แต่จะเท่ากับอัตราส่วนของค่าเหล่านี้

เมื่อกระแสเดียวกันไหลในสองส่วนของวงจรและแรงดันที่ใช้กับพวกมันต่างกัน เป็นที่ชัดเจนว่าส่วนที่ใช้แรงดันที่มากกว่านั้นมีความต้านทานที่มากกว่าตามลำดับ

และถ้าภายใต้การกระทำของแรงดันไฟฟ้าเดียวกัน กระแสที่แตกต่างกันไหลในสองส่วนที่แตกต่างกันของวงจร ดังนั้นในส่วนนี้จะมีกระแสที่เล็กกว่าซึ่งมีความต้านทานมากกว่าเสมอทั้งหมดนี้มาจากการกำหนดพื้นฐานของกฎของโอห์มสำหรับส่วนของวงจร กล่าวคือ ยิ่งกระแสไฟฟ้ามากขึ้น แรงดันไฟฟ้าก็จะยิ่งมากขึ้นและความต้านทานก็จะยิ่งต่ำลง

การคำนวณความต้านทานโดยใช้กฎของโอห์มสำหรับส่วนของวงจรจะแสดงในตัวอย่างต่อไปนี้ ให้ค้นหาความต้านทานของส่วนที่กระแส 50 mA ไหลผ่านที่แรงดัน 40 V แสดงกระแส ในหน่วยแอมแปร์ เราได้ I = 0.05 A หาร 40 ด้วย 0.05 และพบว่าความต้านทานคือ 800 โอห์ม

กฎของโอห์มสามารถมองเห็นได้ในรูปแบบของสิ่งที่เรียกว่า ลักษณะกระแส-แรงดัน... อย่างที่คุณทราบ ความสัมพันธ์แบบสัดส่วนโดยตรงระหว่างปริมาณสองปริมาณคือเส้นตรงที่ผ่านจุดกำเนิด การพึ่งพานี้มักจะเรียกว่าเชิงเส้น

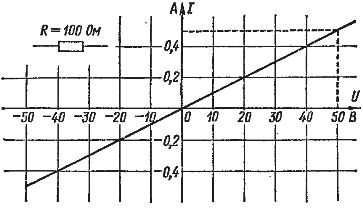
ในรูป 2 แสดงเป็นกราฟตัวอย่างกฎของโอห์มสำหรับส่วนของวงจรที่มีความต้านทาน 100 โอห์ม แกนนอนคือแรงดันเป็นโวลต์และแกนตั้งคือกระแสเป็นแอมแปร์ สามารถเลือกสเกลกระแสและแรงดันได้ตามต้องการ มีการวาดเส้นตรงเพื่อให้แต่ละจุดมีอัตราส่วนแรงดันต่อกระแสเท่ากับ 100 โอห์ม ตัวอย่างเช่น ถ้า U = 50 V ดังนั้น I = 0.5 A และ R = 50: 0.5 = 100 โอห์ม

ข้าว. 2… กฎของโอห์ม (ลักษณะกระแส-แรงดัน)

กราฟของกฎของโอห์มสำหรับค่าลบของกระแสและแรงดันจะเหมือนกัน หมายความว่ากระแสในวงจรไหลเหมือนกันทั้งสองทิศทาง ยิ่งมีความต้านทานมากเท่าใด กระแสไฟฟ้าก็จะยิ่งน้อยลงเท่านั้นที่แรงดันไฟฟ้าที่กำหนด และยิ่งเส้นตรงเคลื่อนที่อย่างระมัดระวังมากขึ้นเท่านั้น

อุปกรณ์ที่มีลักษณะแรงดันกระแสเป็นเส้นตรงที่ผ่านจุดเริ่มต้น นั่นคือ ความต้านทานจะคงที่เมื่อแรงดันหรือกระแสเปลี่ยนแปลงเรียกว่า อุปกรณ์เชิงเส้น... นอกจากนี้ยังใช้เงื่อนไข วงจรเชิงเส้น, ความต้านทานเชิงเส้น

นอกจากนี้ยังมีอุปกรณ์ที่ความต้านทานเปลี่ยนแปลงเมื่อแรงดันหรือกระแสเปลี่ยนแปลง จากนั้นความสัมพันธ์ระหว่างกระแสและแรงดันจะไม่แสดงตามกฎของโอห์ม แต่เป็นวิธีที่ซับซ้อนกว่า สำหรับอุปกรณ์ดังกล่าว ลักษณะกระแส-แรงดันจะไม่เป็นเส้นตรงที่ผ่านจุดเริ่มต้น แต่เป็นเส้นโค้งหรือเส้นประ อุปกรณ์เหล่านี้เรียกว่าไม่ใช่เชิงเส้น

ดูเพิ่มเติมในหัวข้อนี้: การประยุกต์ใช้กฎของโอห์มในทางปฏิบัติ

แผนภาพช่วยจำกฎของโอห์ม