อิเล็กตรอนในสนามไฟฟ้า

การเคลื่อนที่ของอิเล็กตรอนในสนามไฟฟ้าเป็นหนึ่งในกระบวนการทางกายภาพที่สำคัญที่สุดสำหรับวิศวกรรมไฟฟ้า รูป มาดูกันว่าสิ่งนี้เกิดขึ้นในสุญญากาศได้อย่างไร ก่อนอื่น ให้เราพิจารณาตัวอย่างการเคลื่อนที่ของอิเล็กตรอนจากแคโทดไปยังแอโนดในสนามไฟฟ้าที่สม่ำเสมอ

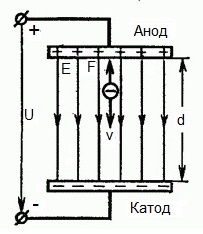
รูปด้านล่างแสดงสถานการณ์ที่ อิเล็กตรอน ออกจากขั้วลบ (แคโทด) ด้วยความเร็วเริ่มต้นเล็กน้อยเล็กน้อย (พุ่งไปที่ศูนย์) และเข้าสู่ ในสนามไฟฟ้าที่สม่ำเสมออยู่ระหว่างสองขั้วไฟฟ้า

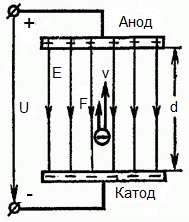
อิเล็กโทรดใช้แรงดันไฟฟ้าคงที่ U และสนามไฟฟ้ามีความแรงเท่ากัน E ระยะห่างระหว่างอิเล็กโทรดเท่ากับ d ในกรณีนี้ แรง F จะกระทำกับอิเล็กตรอนจากด้านข้างของสนาม ซึ่งเป็นสัดส่วนกับประจุของอิเล็กตรอนและความแรงของสนาม:

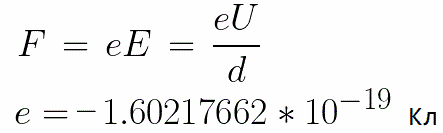
เนื่องจากอิเล็กตรอนมีประจุลบ แรงนี้จะพุ่งตรงไปยังเวกเตอร์ความแรงของสนาม E ดังนั้นอิเล็กตรอนจะถูกเร่งในทิศทางนั้นโดยสนามไฟฟ้า

ความเร่งที่อิเล็กตรอนได้รับนั้นเป็นสัดส่วนกับขนาดของแรง F ที่กระทำกับมัน และแปรผกผันกับมวล m ของอิเล็กตรอนเนื่องจากฟิลด์มีความสม่ำเสมอ ความเร่งสำหรับรูปภาพที่กำหนดจึงสามารถแสดงเป็น:

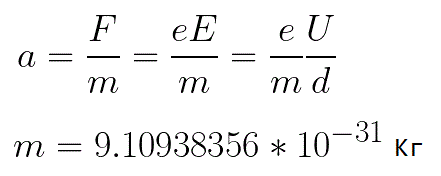
ในสูตรนี้ อัตราส่วนของประจุของอิเล็กตรอนต่อมวลคือประจุเฉพาะของอิเล็กตรอน ซึ่งเป็นปริมาณที่เป็นค่าคงที่ทางกายภาพ:

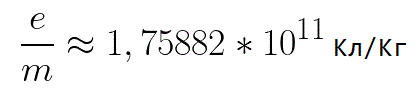
ดังนั้น อิเล็กตรอนจึงอยู่ในสนามไฟฟ้าที่มีความเร่ง เนื่องจากทิศทางของความเร็วเริ่มต้น v0 ตรงกับทิศทางของแรง F ที่ด้านข้างของสนาม ดังนั้น อิเล็กตรอนจึงเคลื่อนที่อย่างสม่ำเสมอ หากไม่มีสิ่งกีดขวาง มันจะเคลื่อนที่ไปตามเส้นทาง d ระหว่างขั้วไฟฟ้าและไปถึงขั้วบวก (ขั้วบวก) ด้วยความเร็วที่แน่นอน v ในขณะที่อิเล็กตรอนมาถึงขั้วบวก พลังงานจลน์ของมันจะเท่ากับ:

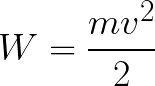
เนื่องจากตลอดเส้นทาง d อิเล็กตรอนถูกเร่งโดยแรงของสนามไฟฟ้า จึงได้รับพลังงานจลน์นี้อันเป็นผลมาจากงานที่ทำโดยแรงที่กระทำด้านข้างของสนาม งานนี้เท่ากับ:

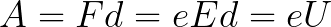
จากนั้นสามารถหาพลังงานจลน์ที่อิเล็กตรอนเคลื่อนที่ในสนามได้ดังนี้

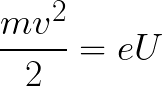
นั่นคือไม่มีอะไรมากไปกว่าการทำงานของพลังภาคสนามเพื่อเร่งอิเล็กตรอนระหว่างจุดที่มีความต่างศักย์ U

ในสถานการณ์เช่นนี้ เพื่อแสดงพลังงานของอิเล็กตรอน จะสะดวกที่จะใช้หน่วยวัดเช่น "อิเล็กตรอนโวลต์" ซึ่งเท่ากับพลังงานของอิเล็กตรอนที่แรงดัน 1 โวลต์ และเนื่องจากประจุอิเล็กตรอนมีค่าคงที่ ดังนั้น 1 อิเล็กโทรโวลต์จึงเป็นค่าคงที่ด้วย:

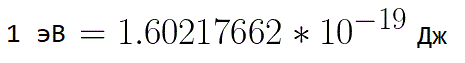
จากสูตรก่อนหน้านี้ คุณสามารถกำหนดความเร็วของอิเล็กตรอนที่จุดใดๆ บนเส้นทางของมันได้อย่างง่ายดายเมื่อเคลื่อนที่ในสนามไฟฟ้าที่มีความเร่ง โดยรู้เฉพาะความต่างศักย์ที่ส่งผ่านไปเมื่อเร่งความเร็ว:

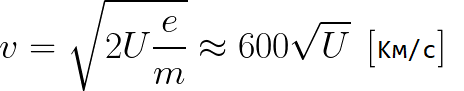
อย่างที่เราเห็น ความเร็วของอิเล็กตรอนในสนามเร่งขึ้นอยู่กับความต่างศักย์ U ระหว่างจุดสิ้นสุดและจุดเริ่มต้นของเส้นทางเท่านั้น

ลองนึกภาพว่าอิเล็กตรอนเริ่มเคลื่อนที่ออกจากแคโทดด้วยความเร็วเล็กน้อย และแรงดันไฟฟ้าระหว่างแคโทดกับแอโนดคือ 400 โวลต์ ในกรณีนี้ เมื่อถึงขั้วบวก ความเร็วของมันจะเท่ากับ:

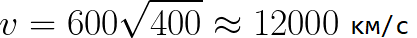
นอกจากนี้ยังง่ายต่อการกำหนดเวลาสำหรับอิเล็กตรอนในการเดินทางระยะทาง d ระหว่างอิเล็กโทรด เมื่อเคลื่อนที่ด้วยความเร่งอย่างสม่ำเสมอจากที่พัก ความเร็วเฉลี่ยจะเท่ากับครึ่งหนึ่งของความเร็วสุดท้าย จากนั้นเวลาของการเร่งความเร็วในสนามไฟฟ้าจะเท่ากับ:

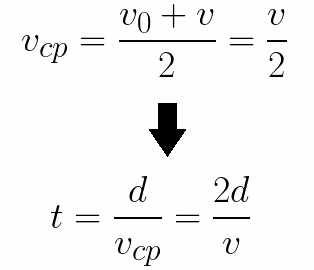
ให้เราพิจารณาตัวอย่างเมื่ออิเล็กตรอนเคลื่อนที่ในสนามไฟฟ้าสม่ำเสมอที่ลดความเร็วลง นั่นคือ สนามถูกกำกับเช่นเดิมแต่อิเล็กตรอนเริ่มเคลื่อนที่ในทิศทางตรงกันข้าม – จากขั้วบวกไปยังขั้วลบ

สมมติว่าอิเล็กตรอนออกจากขั้วบวกด้วยความเร็วเริ่มต้น v และเริ่มเคลื่อนที่ในทิศทางของแคโทด ในกรณีนี้ แรง F ที่กระทำต่ออิเล็กตรอนจากด้านข้างของสนามไฟฟ้าจะพุ่งเข้าหาเวกเตอร์ความเข้มไฟฟ้า E จากแคโทดไปยังแอโนด

มันจะเริ่มลดความเร็วเริ่มต้นของอิเล็กตรอน นั่นคือ สนามจะทำให้อิเล็กตรอนเคลื่อนที่ช้าลง ซึ่งหมายความว่าอิเล็กตรอนภายใต้เงื่อนไขเหล่านี้จะเริ่มเคลื่อนที่อย่างสม่ำเสมอและสม่ำเสมออย่างช้าๆ มีการอธิบายสถานการณ์ดังนี้: "อิเล็กตรอนเคลื่อนที่ในสนามไฟฟ้าที่ชะลอตัวลง"

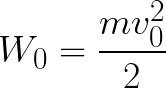
จากขั้วบวก อิเล็กตรอนเริ่มเคลื่อนที่ด้วยพลังงานจลน์ที่ไม่เป็นศูนย์ ซึ่งเริ่มลดลงระหว่างการชะลอตัว เนื่องจากขณะนี้พลังงานถูกใช้ไปกับการเอาชนะแรงที่กระทำจากสนามบนอิเล็กตรอน

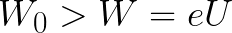
ถ้าพลังงานจลน์เริ่มต้นของอิเล็กตรอนเมื่อออกจากขั้วบวกมีค่ามากกว่าพลังงานที่สนามจะต้องใช้ไปในทันทีเพื่อเร่งอิเล็กตรอนให้เคลื่อนที่จากขั้วลบไปยังขั้วบวก (ดังตัวอย่างแรก) อิเล็กตรอนก็จะ เดินทางเป็นระยะทาง d และในที่สุดจะถึงแคโทดแม้จะเบรกก็ตาม

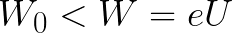
ถ้าพลังงานจลน์เริ่มต้นของอิเล็กตรอนน้อยกว่าค่าวิกฤตินี้ อิเล็กตรอนจะไปไม่ถึงแคโทด เมื่อถึงจุดหนึ่งมันจะหยุด จากนั้นจึงเริ่มเคลื่อนที่ด้วยความเร่งสม่ำเสมอกลับไปที่ขั้วบวก เป็นผลให้สนามจะคืนพลังงานที่ใช้ในกระบวนการหยุดกลับคืนสู่สนาม

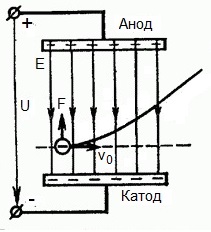
แต่ถ้าอิเล็กตรอนบินด้วยความเร็ว v0 ในบริเวณที่มีการกระทำของสนามไฟฟ้าเป็นมุมฉากล่ะ? เห็นได้ชัดว่า แรงที่ด้านข้างของสนามในบริเวณนี้พุ่งเข้าหาอิเล็กตรอนจากแคโทดไปยังแอโนด นั่นคือ ต้านเวกเตอร์ความแรงของสนามไฟฟ้า E

ซึ่งหมายความว่าตอนนี้อิเล็กตรอนมีส่วนประกอบของการเคลื่อนที่สองส่วน: ส่วนแรก - ด้วยความเร็ว v0 ตั้งฉากกับสนาม ส่วนที่สอง - เร่งอย่างสม่ำเสมอภายใต้การกระทำของแรงจากด้านข้างของสนามที่พุ่งตรงไปยังขั้วบวก

ปรากฎว่าเมื่อบินเข้าสู่สนามรบแล้วอิเล็กตรอนจะเคลื่อนที่ไปตามวิถีพาราโบลา แต่หลังจากบินออกจากขอบเขตของสนามแล้ว อิเล็กตรอนจะยังคงเคลื่อนที่อย่างสม่ำเสมอต่อไปโดยความเฉื่อยตามวิถีการเคลื่อนที่เป็นเส้นตรง