กระแสลัดวงจร ซึ่งกำหนดขนาดของกระแสลัดวงจร

บทความนี้จะมุ่งเน้นไปที่การลัดวงจรในเครือข่ายไฟฟ้า เราจะพิจารณาตัวอย่างทั่วไปของการลัดวงจร วิธีการคำนวณกระแสลัดวงจร ให้ความสนใจกับความสัมพันธ์ระหว่างความต้านทานอุปนัยและกำลังรับการจัดอันดับของหม้อแปลงเมื่อคำนวณกระแสลัดวงจร และยังให้สูตรง่ายๆ เฉพาะสำหรับการคำนวณเหล่านี้

เมื่อออกแบบการติดตั้งระบบไฟฟ้าจำเป็นต้องทราบค่าของกระแสลัดวงจรแบบสมมาตรสำหรับจุดต่าง ๆ ของวงจรสามเฟส ค่าของกระแสสมมาตรวิกฤตเหล่านี้ทำให้สามารถคำนวณพารามิเตอร์ของสายเคเบิล สวิตช์เกียร์ อุปกรณ์ป้องกันที่เลือก เป็นต้น

ถัดไป ให้พิจารณากระแสลัดวงจรความต้านทานศูนย์สามเฟสที่ป้อนผ่านหม้อแปลงกระจายแบบกระจายทั่วไป ภายใต้สภาวะปกติ ความเสียหายประเภทนี้ (การลัดวงจรของการเชื่อมต่อโบลต์) เป็นสิ่งที่อันตรายที่สุดและการคำนวณนั้นง่ายมากการคำนวณอย่างง่ายช่วยให้ได้ผลลัพธ์ที่แม่นยำเพียงพอภายใต้กฎบางอย่างซึ่งเป็นที่ยอมรับสำหรับการออกแบบการติดตั้งระบบไฟฟ้า

กระแสลัดวงจรในขดลวดทุติยภูมิของหม้อแปลงระบบจำหน่ายแบบขั้นบันได ในการประมาณครั้งแรก ความต้านทานของวงจรไฟฟ้าแรงสูงถือว่ามีค่าน้อยมาก ดังนั้นจึงสามารถละเลยได้:

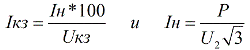
ที่นี่ P คือกำลังไฟฟ้าที่กำหนดในหน่วยโวลต์แอมแปร์, U2 คือแรงดันเฟสต่อเฟสของขดลวดทุติยภูมิที่ไม่มีโหลด, In คือกระแสไฟฟ้าที่กำหนดในหน่วยแอมแปร์, Isc คือกระแสลัดวงจรในหน่วยแอมแปร์, Usc คือกระแสลัดวงจร แรงดันวงจรเป็นเปอร์เซ็นต์

ตารางด้านล่างแสดงแรงดันไฟฟ้าลัดวงจรทั่วไปสำหรับหม้อแปลงสามเฟสสำหรับขดลวด HV 20 kV

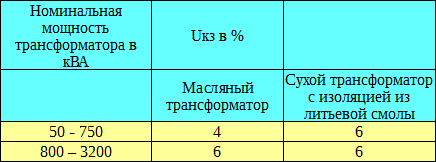
ตัวอย่างเช่น หากเราพิจารณากรณีที่ป้อนหม้อแปลงหลายตัวขนานกับบัส ค่าของกระแสลัดวงจรที่จุดเริ่มต้นของสายที่เชื่อมต่อกับบัสสามารถรับได้เท่ากับผลรวมของการลัดวงจร กระแสซึ่งก่อนหน้านี้คำนวณแยกกันสำหรับหม้อแปลงแต่ละตัว

เมื่อป้อนหม้อแปลงทั้งหมดจากเครือข่ายไฟฟ้าแรงสูงเดียวกัน ค่าของกระแสลัดวงจรเมื่อรวมเข้าด้วยกันจะให้ค่าที่สูงกว่าที่ปรากฏจริงเล็กน้อย ความต้านทานของบัสบาร์และสวิตช์ถูกละเลย

ให้หม้อแปลงมีกำลังไฟ 400 kVA แรงดันไฟฟ้าของขดลวดทุติยภูมิคือ 420 V ถ้าเราใช้ Usc = 4% แล้ว:

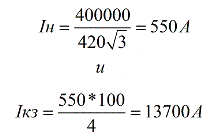
รูปด้านล่างแสดงคำอธิบายสำหรับตัวอย่างนี้

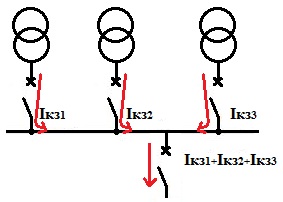
ความถูกต้องของค่าที่ได้จะเพียงพอในการคำนวณการติดตั้งไฟฟ้า

กระแสไฟลัดวงจรสามเฟสที่จุดติดตั้งด้านแรงดันต่ำ:

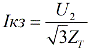
ที่นี่: U2 คือแรงดันไม่มีโหลดระหว่างเฟสของขดลวดทุติยภูมิของหม้อแปลง Zt — อิมพีแดนซ์ของวงจรที่อยู่เหนือจุดที่เกิดข้อผิดพลาด จากนั้นพิจารณาวิธีการหา Zt

แต่ละส่วนของการติดตั้ง ไม่ว่าจะเป็นเครือข่าย สายไฟ ตัวหม้อแปลงเอง เซอร์กิตเบรกเกอร์หรือบัสบาร์ มีอิมพีแดนซ์ Z ของตัวเองซึ่งประกอบด้วยแอกทีฟ R และรีแอกทีฟ X

ความต้านทานต่อตัวเก็บประจุไม่ได้มีบทบาทที่นี่ Z, R และ X แสดงเป็นโอห์มและคำนวณเป็นด้านของสามเหลี่ยมมุมฉากดังแสดงในรูปด้านล่าง อิมพีแดนซ์คำนวณตามกฎสามเหลี่ยมมุมฉาก

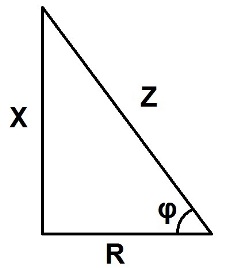
ตารางถูกแบ่งออกเป็นส่วนต่าง ๆ เพื่อค้นหา X และ R สำหรับแต่ละส่วนเพื่อให้การคำนวณสะดวก สำหรับวงจรอนุกรม ค่าความต้านทานจะถูกเพิ่มง่ายๆ และผลลัพธ์คือ Xt และ RT ความต้านทานรวม Zt ถูกกำหนดโดยทฤษฎีบทพีทาโกรัสสำหรับสามเหลี่ยมมุมฉากตามสูตร:

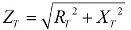
เมื่อเชื่อมต่อส่วนขนานกัน การคำนวณจะดำเนินการสำหรับตัวต้านทานที่เชื่อมต่อแบบขนาน หากส่วนขนานที่รวมกันมีรีแอกแตนซ์หรือความต้านทานแบบแอกทีฟ จะได้ค่าความต้านทานรวมที่เท่ากัน:

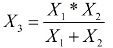
Xt ไม่ได้คำนึงถึงอิทธิพลของตัวเหนี่ยวนำ และถ้าตัวเหนี่ยวนำที่อยู่ติดกันมีอิทธิพลต่อกันและกัน ค่าความเหนี่ยวนำที่แท้จริงจะสูงขึ้น ควรสังเกตว่าการคำนวณ Xz นั้นเกี่ยวข้องกับวงจรอิสระที่แยกจากกันเท่านั้น นั่นคือไม่มีอิทธิพลของการเหนี่ยวนำร่วมกัน หากวงจรคู่ขนานอยู่ใกล้กัน ความต้านทาน Xs จะสูงขึ้นอย่างเห็นได้ชัด

พิจารณาเครือข่ายที่เชื่อมต่อกับอินพุตของหม้อแปลง step-down Isc กระแสลัดวงจรสามเฟสหรือ Psc กำลังไฟฟ้าลัดวงจรถูกกำหนดโดยผู้ผลิตไฟฟ้า แต่จากข้อมูลเหล่านี้สามารถหาค่าความต้านทานสมมูลทั้งหมดได้ อิมพีแดนซ์สมมูล ซึ่งส่งผลพร้อมกันในด้านแรงดันต่ำ:

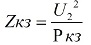
Psc-แหล่งจ่ายไฟลัดวงจรสามเฟส, แรงดัน U2-ไม่มีโหลดของวงจรแรงดันต่ำ

ตามกฎแล้วส่วนประกอบที่ใช้งานอยู่ของความต้านทานของเครือข่ายไฟฟ้าแรงสูง - Ra - มีขนาดเล็กมากและไม่มีนัยสำคัญเมื่อเทียบกับความต้านทานแบบอุปนัย ตามอัตภาพ Xa เท่ากับ 99.5% ของ Za และ Ra เท่ากับ 10% ของ Xa ตารางด้านล่างแสดงตัวเลขโดยประมาณสำหรับค่าเหล่านี้สำหรับหม้อแปลง 500 MVA และ 250 MVA

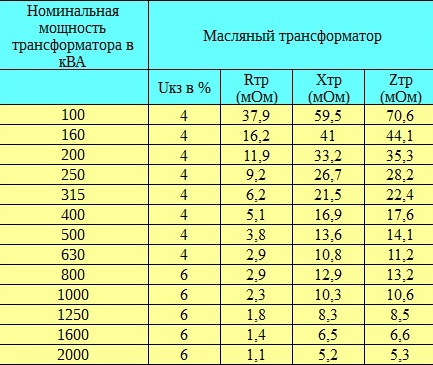
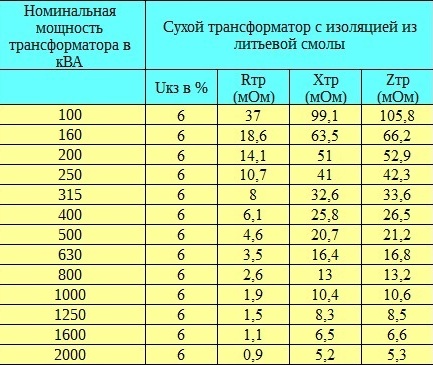
Full Ztr — ความต้านทานของหม้อแปลงด้านแรงดันต่ำ:

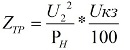
Pn — กำลังไฟของหม้อแปลงเป็นกิโลโวลต์-แอมแปร์

ขึ้นอยู่กับความต้านทานที่ใช้งานของขดลวด การสูญเสียพลังงาน.

เมื่อทำการคำนวณโดยประมาณ Rtr จะถูกละเลยและ Ztr = Xtr

หากต้องพิจารณาเบรกเกอร์แรงดันต่ำ ให้พิจารณาอิมพีแดนซ์ของเบรกเกอร์เหนือจุดลัดวงจร ความต้านทานอุปนัยมีค่าเท่ากับ 0.00015 โอห์มต่อสวิตช์และส่วนประกอบที่ใช้งานอยู่จะถูกละเลย

สำหรับบัสบาร์ ความต้านทานแบบแอกทีฟนั้นน้อยมาก ในขณะที่ส่วนประกอบปฏิกิริยามีการกระจายที่ประมาณ 0.00015 โอห์มต่อเมตรของความยาว และเมื่อระยะห่างระหว่างบัสบาร์เพิ่มขึ้นเป็นสองเท่า ค่ารีแอกแตนซ์จะเพิ่มขึ้นเพียง 10% ผู้ผลิตระบุพารามิเตอร์ของสายเคเบิล

สำหรับมอเตอร์สามเฟสในขณะที่ไฟฟ้าลัดวงจรจะเข้าสู่โหมดเครื่องกำเนิดไฟฟ้าและกระแสไฟฟ้าลัดวงจรในขดลวดจะประมาณ Isc = 3.5 * In ในมอเตอร์เฟสเดียว การเพิ่มขึ้นของกระแสในขณะที่ไฟฟ้าลัดวงจรนั้นเล็กน้อย

ส่วนโค้งที่มักจะมาพร้อมกับการลัดวงจรมีความต้านทานที่ไม่คงที่ แต่ค่าเฉลี่ยนั้นต่ำมาก แต่แรงดันตกคร่อมส่วนโค้งมีขนาดเล็ก ดังนั้นกระแสจึงลดลงจริงประมาณ 20% ซึ่งอำนวยความสะดวกในการทำงาน ของเซอร์กิตเบรกเกอร์โดยไม่รบกวนการทำงานของเบรกเกอร์ โดยไม่ส่งผลกระทบต่อกระแสตัดวงจรโดยเฉพาะ

กระแสลัดวงจรที่ปลายสายรับจะสัมพันธ์กับกระแสลัดวงจรที่ปลายสายจ่าย แต่ส่วนตัดขวางและวัสดุของสายส่งสัญญาณ ตลอดจนความยาวจะถูกนำมาพิจารณาด้วย บัญชี. เมื่อมีความคิดที่จะต่อต้าน ใครๆ ก็สามารถทำการคำนวณอย่างง่ายนี้ได้ เราหวังว่าบทความของเราจะเป็นประโยชน์สำหรับคุณ