ระบบของหน่วยสัมพัทธ์

เพื่อให้การคำนวณง่ายขึ้นเมื่อคำนวณพารามิเตอร์ในระบบส่งกำลัง ระบบจะใช้หน่วยสัมพัทธ์ วิธีนี้เกี่ยวข้องกับการแสดงค่าปัจจุบันของค่าระบบในแง่ของค่าฐาน (ฐาน) ที่คิดเป็นหน่วย

ดังนั้นค่าสัมพัทธ์จะแสดงเป็นตัวคูณของค่าฐาน (กระแส แรงดัน ความต้านทาน กำลัง ฯลฯ) และไม่ขึ้นอยู่กับระดับแรงดันที่แสดงเป็นหน่วยสัมพัทธ์ ในวรรณคดีอังกฤษ หน่วยสัมพัทธ์หมายถึง pu หรือ p.u (จากระบบหน่วย — ระบบหน่วยสัมพัทธ์).

ตัวอย่างเช่น สำหรับหม้อแปลงประเภทเดียวกัน แรงดันตก อิมพีแดนซ์ และการสูญเสียจะแตกต่างกันในค่าสัมบูรณ์ที่แรงดันที่ใช้ต่างกัน แต่ในขนาดที่สัมพันธ์กันพวกเขาจะยังคงเหมือนเดิม เมื่อคำนวณเสร็จแล้วผลลัพธ์จะถูกแปลงกลับเป็นหน่วยระบบได้อย่างง่ายดาย (เป็นแอมแปร์, เป็นโวลต์, เป็นโอห์ม, เป็นวัตต์ ฯลฯ ) เนื่องจากทราบค่าฐานที่เปรียบเทียบค่าปัจจุบันในขั้นต้น

ตามกฎแล้วหน่วยสัมพัทธ์นั้นสะดวกสำหรับการคำนวณกำลังส่ง แต่บ่อยครั้งที่มีการระบุพารามิเตอร์ของเครื่องกำเนิดมอเตอร์และหม้อแปลงในหน่วยสัมพัทธ์ดังนั้นวิศวกรทุกคนจึงควรคุ้นเคยกับแนวคิดของหน่วยสัมพัทธ์ หน่วยของกำลัง กระแส แรงดัน อิมพีแดนซ์ อนุญาติให้ใช้ในระบบหน่วยสัมพัทธ์ กำลังไฟฟ้าและแรงดันไฟฟ้าเป็นปริมาณอิสระที่กำหนดโดยคุณสมบัติของระบบพลังงานจริง

ค่าเครือข่ายทั้งหมดของระบบสามารถแสดงเป็นค่าทวีคูณของค่าฐานที่เลือก ดังนั้นถ้าเราพูดถึงพลังงานก็สามารถเลือกกำลังไฟของหม้อแปลงเป็นค่าพื้นฐานได้ มันเกิดขึ้นที่พลังงานที่ได้รับในช่วงเวลาหนึ่งในรูปแบบของค่าสัมพัทธ์ช่วยอำนวยความสะดวกในการคำนวณอย่างมาก พื้นฐานของแรงดันไฟฟ้าคือแรงดันบัสที่กำหนด ฯลฯ

โดยทั่วไปแล้ว บริบทจะช่วยให้คุณเข้าใจว่ามีการกล่าวถึงค่าสัมพัทธ์ใดบ้าง และแม้แต่การมีสัญลักษณ์ "pu" เหมือนกันในวรรณคดีอังกฤษก็ไม่ทำให้คุณสับสน

ดังนั้นปริมาณทางกายภาพของระบบทั้งหมดจึงถูกตั้งชื่อ แต่เมื่อเราแปลเป็นหน่วยสัมพัทธ์ (จริง ๆ แล้วเป็นเปอร์เซ็นต์) ลักษณะของการคำนวณทางทฤษฎีจะเป็นแบบทั่วไป

ค่าสัมพัทธ์ของปริมาณทางกายภาพบางอย่างถูกเข้าใจว่าเป็นความสัมพันธ์ของค่าฐานบางอย่าง นั่นคือ ค่าที่เลือกเป็นหน่วยสำหรับการวัดที่กำหนด ค่าสัมพัทธ์มีเครื่องหมายดอกจันด้านล่าง

บ่อยครั้งที่ใช้ค่าพื้นฐานต่อไปนี้ในการคำนวณ: ความต้านทานพื้นฐาน, กระแสพื้นฐาน, แรงดันพื้นฐานและพลังงานพื้นฐาน

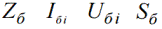
ตัวห้อย «b» ระบุว่านี่เป็นค่าพื้นฐาน

จากนั้นหน่วยการวัดสัมพัทธ์จะถูกเรียกว่าพื้นฐานสัมพัทธ์:

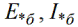
เครื่องหมายดอกจันระบุค่าสัมพัทธ์ ตัวอักษร «b» - ฐาน EMF ค่อนข้างพื้นฐาน กระแสค่อนข้างพื้นฐาน ฯลฯ และหน่วยฐานสัมพัทธ์จะถูกกำหนดโดยนิพจน์ต่อไปนี้:

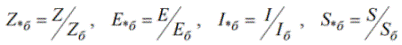
ตัวอย่างเช่น ในการวัดความเร็วเชิงมุม ความเร็วซิงโครนัสเชิงมุมถือเป็นเอกภาพ ดังนั้น ความเร็วเชิงมุมซิงโครนัสจะเท่ากับความเร็วเชิงมุมมูลฐาน

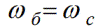
จากนั้นความเร็วเชิงมุมตามอำเภอใจสามารถแสดงเป็นหน่วยสัมพัทธ์ได้:

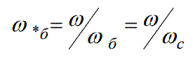
ดังนั้น ความสัมพันธ์ต่อไปนี้อาจถูกนำมาใช้เป็นพื้นฐานสำหรับการเชื่อมโยงฟลักซ์และสำหรับการเหนี่ยวนำ:

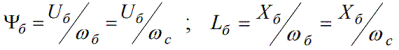
ที่นี่การเชื่อมโยงฟลักซ์หลักคือการเชื่อมโยงฟลักซ์ที่ก่อให้เกิดความเครียดหลักที่ความเร็วเชิงมุมหลัก

ดังนั้นหากใช้ความเร็วเชิงมุมแบบซิงโครนัสเป็นพื้นฐานแล้ว:

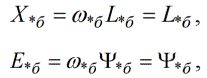
ในหน่วยสัมพัทธ์ emf เท่ากับฟลักซ์และความต้านทานอุปนัยเท่ากับความเหนี่ยวนำ นี่เป็นเพราะหน่วยพื้นฐานได้รับการคัดเลือกอย่างเหมาะสม

จากนั้นพิจารณาแรงดันเฟสในหน่วยสัมพัทธ์และพื้นฐาน:

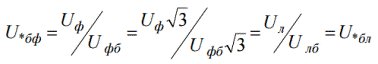
มันง่ายที่จะเห็นว่าแรงดันเฟสในหน่วยมูลฐานสัมพัทธ์จะเท่ากับแรงดันมูลฐานสัมพัทธ์เชิงเส้น ในทำนองเดียวกัน ค่าของแอมพลิจูดของความเค้นในหน่วยสัมพัทธ์จะเท่ากับค่าที่มีประสิทธิภาพ:

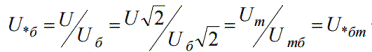
จากการพึ่งพาเหล่านี้เห็นได้ชัดว่าในหน่วยสัมพัทธ์แม้แต่กำลังของสามเฟสและกำลังของเฟสเดียวก็เท่ากันและกระแสกระตุ้นฟลักซ์และแรงเคลื่อนไฟฟ้าของเครื่องกำเนิดไฟฟ้าก็เท่ากันเช่นกัน

โปรดทราบว่าสำหรับแต่ละองค์ประกอบของวงจร ความต้านทานสัมพัทธ์จะเท่ากับแรงดันตกคร่อมภายใต้เงื่อนไขของกำลังไฟที่กำหนดที่จ่ายให้กับวงจร

เมื่อคำนวณกระแสลัดวงจร จะใช้พารามิเตอร์หลัก 4 ตัว ได้แก่ กระแส แรงดัน ความต้านทาน และกำลัง ค่าพื้นฐานของแรงดันและพลังงานจะถือว่าเป็นอิสระจากกัน จากนั้นค่าความต้านทานและกระแสพื้นฐานจะถูกแสดงออกมา จากสมการพลังงานของเครือข่ายสามเฟส - กระแสแล้ว กฎของโอห์ม - ความต้านทาน:

เนื่องจากสามารถเลือกค่าฐานได้ตามอำเภอใจ ปริมาณทางกายภาพเดียวกันที่แสดงเป็นหน่วยสัมพัทธ์จึงมีค่าตัวเลขต่างกันได้ ดังนั้น ความต้านทานสัมพัทธ์ของเครื่องกำเนิดไฟฟ้า มอเตอร์ หม้อแปลง จะถูกตั้งค่าเป็นหน่วยสัมพัทธ์โดยการป้อนหน่วยค่าสัมพัทธ์ Sn — กำลังไฟเล็กน้อย Un — แรงดันเล็กน้อย ค่าเล็กน้อยสัมพัทธ์เขียนด้วยดัชนี «n»:

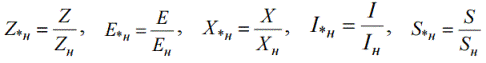
เพื่อหาค่าความต้านทานและกระแสที่กำหนด จะใช้สูตรมาตรฐาน:

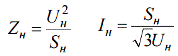
เพื่อสร้างความสัมพันธ์ระหว่างหน่วยสัมพัทธ์และปริมาณที่กำหนด ก่อนอื่นเราจะแสดงความสัมพันธ์ระหว่างฐานสัมพัทธ์และปริมาณฐาน:

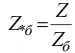
ลองเขียนความต้านทานพื้นฐานในรูปของพลังงานและการแทนที่:

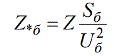
คุณจึงสามารถแปลค่าที่ระบุเป็นค่าฐานสัมพัทธ์ได้

และในทำนองเดียวกัน คุณสามารถสร้างความสัมพันธ์ระหว่างหน่วยนามสัมพัทธ์กับคำนามได้:

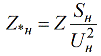
ในการคำนวณค่าความต้านทานในหน่วยที่กำหนดชื่อด้วยค่าเล็กน้อยสัมพัทธ์ที่ทราบ ให้ใช้สูตรต่อไปนี้:

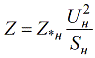
ความสัมพันธ์ระหว่างหน่วยนามสัมพัทธ์และหน่วยฐานสัมพัทธ์ถูกกำหนดโดยสูตรต่อไปนี้:

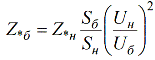
เมื่อใช้สูตรนี้ หน่วยนามสัมพัทธ์สามารถแปลงเป็นหน่วยฐานสัมพัทธ์ได้

ในระบบไฟฟ้า ให้ตั้งค่าเพื่อจำกัดกระแสลัดวงจร เครื่องปฏิกรณ์จำกัดในปัจจุบันอันที่จริง — ตัวเหนี่ยวนำเชิงเส้น พวกเขาได้รับแรงดันไฟฟ้าและกระแสไฟฟ้าที่กำหนด แต่ไม่ได้พลังงาน

กำหนดว่า

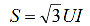
และการแปลงนิพจน์ข้างต้นสำหรับค่าความต้านทานฐานสัมพัทธ์และสัมพัทธ์ เราได้รับ:

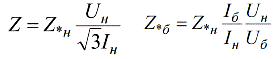
ค่าสัมพัทธ์สามารถแสดงเป็นเปอร์เซ็นต์: