แรงแม่เหล็กคืออะไร กฎของฮอปกินสัน

ในช่วงครึ่งหลังของศตวรรษที่ 19 นักฟิสิกส์ชาวอังกฤษ John Hopkinson และ Edward Hopkinson น้องชายของเขา ได้พัฒนาทฤษฎีทั่วไปของวงจรแม่เหล็ก โดยได้สูตรทางคณิตศาสตร์ที่เรียกว่า "สูตรของ Hopkinson" หรือกฎของ Hopkinson ซึ่งคล้ายกับกฎของโอห์ม (ใช้ เพื่อคำนวณวงจรไฟฟ้า)

ดังนั้น หากกฎคลาสสิกของโอห์มอธิบายความสัมพันธ์ระหว่างกระแสและแรงเคลื่อนไฟฟ้า (EMF) ทางคณิตศาสตร์ กฎของฮอปกินสันก็แสดงความสัมพันธ์ระหว่างฟลักซ์แม่เหล็กกับสิ่งที่เรียกว่า แรงเคลื่อนไฟฟ้า (MDF).

เป็นผลให้มันกลายเป็นว่า แรงเคลื่อนไฟฟ้าเป็นปริมาณทางกายภาพที่แสดงลักษณะความสามารถของกระแสไฟฟ้าในการสร้างฟลักซ์แม่เหล็ก และกฎของฮอปกินสันในเรื่องนี้สามารถนำมาใช้ในการคำนวณวงจรแม่เหล็กได้สำเร็จ เนื่องจาก MDF ในวงจรแม่เหล็กมีความคล้ายคลึงกับ EMF ในวงจรไฟฟ้า วันที่ค้นพบกฎของฮอปกินสันถือเป็นปี พ.ศ. 2429

ขนาดของแรงแม่เหล็ก (MDF) เริ่มต้นวัดเป็นแอมแปร์หรือหากเรากำลังพูดถึงขดลวดที่มีกระแสหรือแม่เหล็กไฟฟ้าเพื่อความสะดวกในการคำนวณให้ใช้นิพจน์เป็นแอมแปร์เทิร์น:

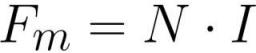
โดยที่ Fm คือแรงแม่เหล็กในขดลวด [แอมแปร์ * รอบ] N คือจำนวนรอบในขดลวด [รอบ] I คือปริมาณกระแสในแต่ละรอบของขดลวด [แอมแปร์]

หากคุณป้อนค่าฟลักซ์แม่เหล็กที่นี่ กฎของฮอปกินสันสำหรับวงจรแม่เหล็กจะอยู่ในรูปแบบ:

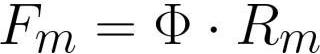
โดยที่ Fm คือแรงเคลื่อนแม่เหล็กในขดลวด [แอมแปร์ * เทิร์น], F คือฟลักซ์แม่เหล็ก [เวเบอร์] หรือ [เฮนรี่ * แอมแปร์], Rm คือความต้านทานแม่เหล็กของตัวนำฟลักซ์แม่เหล็ก [แอมแปร์ * เทิร์น / เวเบอร์] หรือ [ เทิร์น / เฮนรี่] .

การกำหนดข้อความของกฎของฮอปกินสันเดิมมีดังต่อไปนี้: "ในวงจรแม่เหล็กที่ไม่มีเส้นแบ่ง ฟลักซ์แม่เหล็กจะเป็นสัดส่วนโดยตรงกับแรงเคลื่อนไฟฟ้าและแปรผกผันกับความต้านทานแม่เหล็กทั้งหมด" นั่นคือกฎนี้กำหนดความสัมพันธ์ระหว่างแรงแม่เหล็ก ความฝืน และฟลักซ์แม่เหล็กในวงจร:

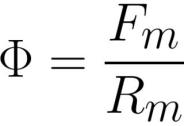
ที่นี่: F คือฟลักซ์แม่เหล็ก [เวเบอร์] หรือ [เฮนรี * แอมแปร์], Fm คือแรงเคลื่อนแม่เหล็กในขดลวด [แอมแปร์ * การปฏิวัติ], Rm คือความต้านทานแม่เหล็กของตัวนำฟลักซ์แม่เหล็ก [แอมแปร์ * การปฏิวัติ / เวเบอร์] หรือ [ เทิร์น / เฮนรี่] .

สิ่งสำคัญคือต้องสังเกตว่าในความเป็นจริงแล้วแรงแม่เหล็ก (MDF) มีความแตกต่างพื้นฐานจากแรงเคลื่อนไฟฟ้า (EMF) ซึ่งประกอบด้วยข้อเท็จจริงที่ว่าไม่มีอนุภาคเคลื่อนที่โดยตรงในฟลักซ์แม่เหล็ก ในขณะที่กระแสที่เกิดขึ้นภายใต้การกระทำของ EMF รับการเคลื่อนที่ของอนุภาคที่มีประจุ เช่น อิเล็กตรอนในเส้นลวดโลหะ อย่างไรก็ตามแนวคิดของ MDS ช่วยแก้ปัญหาการคำนวณวงจรแม่เหล็ก

ตัวอย่างเช่น ลองพิจารณาวงจรแม่เหล็กแบบไม่แยกสายที่มีแอกของพื้นที่หน้าตัด S ซึ่งเท่ากันตลอดความยาวของวงจร และวัสดุของแอกมีการซึมผ่านของแม่เหล็ก mu

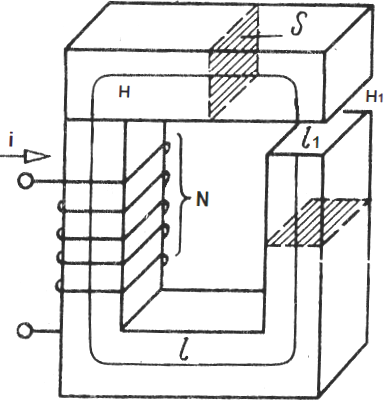
ช่องว่างในแอก - วัสดุที่แตกต่างกัน การซึมผ่านของแม่เหล็ก ซึ่ง mu1. ขดลวดที่วางอยู่บนแอกมี N รอบ กระแส i ไหลผ่านแต่ละรอบของขดลวด เราใช้ทฤษฎีบทการไหลเวียนของสนามแม่เหล็กกับเส้นกึ่งกลางของแอก:

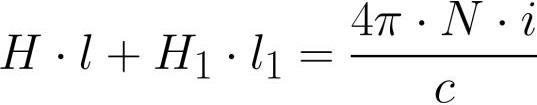
โดยที่: H คือความแรงของสนามแม่เหล็กภายในแอก, H1 คือความแรงของสนามแม่เหล็กภายในช่องว่าง, l คือความยาวกึ่งกลางของการเหนี่ยวนำแอก (โดยไม่มีช่องว่าง), l1 คือความยาวของช่องว่าง

เนื่องจากฟลักซ์แม่เหล็กภายในแอกและภายในช่องว่างมีค่าเท่ากัน (เนื่องจากความต่อเนื่องของเส้นเหนี่ยวนำแม่เหล็ก) หลังจากเขียน Ф = BS และ В = mu * H เราจะเขียนความแรงของสนามแม่เหล็กโดยละเอียด และหลังจากแทนที่สิ่งนี้ในสูตรด้านบน:

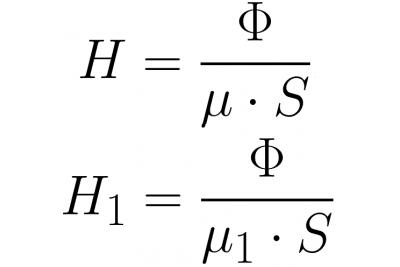
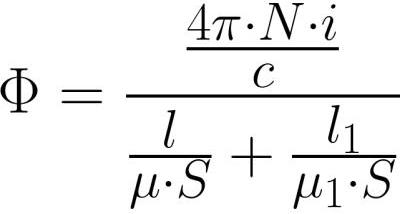
เป็นเรื่องง่ายที่จะเห็นว่า MDS เช่นเดียวกับ EMF ในกฎของโอห์มสำหรับวงจรไฟฟ้า

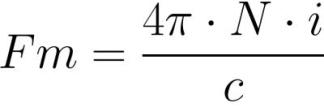
ที่นี่มีบทบาทของแรงเคลื่อนไฟฟ้าและความต้านทานแม่เหล็ก

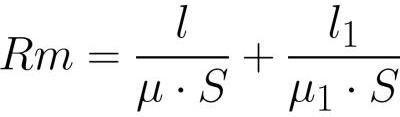
บทบาทของการต่อต้าน (โดยการเปรียบเทียบ ด้วยกฎของโอห์มแบบคลาสสิก).