การคำนวณความต้านทานของลวด

ในทางปฏิบัติมักจำเป็นต้องคำนวณความต้านทานของสายไฟต่างๆ สามารถทำได้โดยใช้สูตรหรือตามข้อมูลที่กำหนดในตาราง 1.

อิทธิพลของวัสดุตัวนำจะถูกนำมาพิจารณาโดยใช้ความต้านทานที่ระบุโดยตัวอักษรกรีก ? และเป็นตัวแทน ความต้านทานของลวด ความยาว 1 ม. และพื้นที่หน้าตัด 1 ตร.มม. ความต้านทานต่ำสุด? = 0.016 โอห์ม • mm2 / m มีสีเงิน เราให้ค่าเฉลี่ยของ coNSrotation เฉพาะของสายไฟบางเส้น:

เงิน — 0.016, ตะกั่ว — 0.21, ทองแดง — 0.017, นิกเกิล — 0.42, อะลูมิเนียม — 0.026, แมงกานีส — 0.42, ทังสเตน — 0.055, Constantan — 0.5, สังกะสี — 0.06, ปรอท — 0, 96, ทองเหลือง — 0.07, Nichrome — 1.05, เหล็ก — 0.1, Fehral -1.2, สารเรืองแสงสีบรอนซ์ — 0.11, Chromal — 1.45

ด้วยปริมาณสิ่งเจือปนที่แตกต่างกันและด้วยอัตราส่วนที่แตกต่างกันของส่วนประกอบที่ประกอบกันเป็นโลหะผสมรีโอสแตท ความต้านทานอาจเปลี่ยนแปลงได้เล็กน้อย

ความต้านทานคำนวณโดยสูตร:

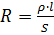
โดยที่ R คือความต้านทาน โอห์ม; ความต้านทาน (โอห์ม • mm2) / m; ล. — ความยาวของลวด, ม.; s - พื้นที่หน้าตัดของเส้นลวด mm2

หากทราบเส้นผ่านศูนย์กลางของเส้นลวด d พื้นที่หน้าตัดจะเท่ากับ:

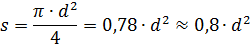
วิธีที่ดีที่สุดคือวัดเส้นผ่านศูนย์กลางของเส้นลวดโดยใช้ไมโครมิเตอร์ แต่ถ้าไม่มีให้หมุนลวด 10 หรือ 20 รอบให้แน่นด้วยดินสอแล้ววัดความยาวของขดลวดด้วยไม้บรรทัด โดยการหารความยาวของขดลวดด้วยจำนวนรอบ เราจะหาเส้นผ่านศูนย์กลางของเส้นลวด

ในการกำหนดความยาวของเส้นลวดที่มีเส้นผ่านศูนย์กลางที่ทราบของวัสดุที่ต้องการเพื่อให้ได้ค่าความต้านทานที่ต้องการ ให้ใช้สูตร

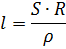
ตารางที่ 1.

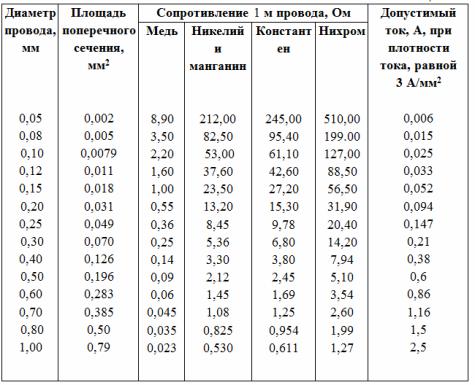
บันทึก. 1. ควรนำข้อมูล Wire ที่ไม่ได้ระบุไว้ในตารางเป็นค่าเฉลี่ยบางส่วน ตัวอย่างเช่น สำหรับลวดนิกเกิลที่มีเส้นผ่านศูนย์กลาง 0.18 มม. สามารถสันนิษฐานได้อย่างคร่าว ๆ ว่าพื้นที่หน้าตัดคือ 0.025 มม. 2 ความต้านทานต่อเมตรคือ 18 โอห์ม และกระแสที่อนุญาตคือ 0.075 A

2. สำหรับค่าความหนาแน่นกระแสที่แตกต่างกัน ข้อมูลในคอลัมน์สุดท้ายควรเปลี่ยนตามนั้น ตัวอย่างเช่น ที่ความหนาแน่นกระแส 6 A / mm2 ควรเพิ่มเป็นสองเท่า

ตัวอย่างที่ 1 จงหาความต้านทานของลวดทองแดงยาว 30 ม. ที่มีเส้นผ่านศูนย์กลาง 0.1 มม.

คำตอบ. กำหนดตามตาราง 1 ความต้านทานของลวดทองแดง 1 ม. มีค่าเท่ากับ 2.2 โอห์ม ดังนั้นความต้านทานของลวด 30 ม. จะเป็น R = 30 • 2.2 = 66 โอห์ม

การคำนวณตามสูตรให้ผลลัพธ์ดังต่อไปนี้: พื้นที่หน้าตัดของเส้นลวด: s = 0.78 • 0.12 = 0.0078 mm2 เนื่องจากความต้านทานของทองแดงเท่ากับ 0.017 (โอห์ม • มม.2) / ม. เราจึงได้ R = 0.017 • 30 / 0.0078 = 65.50 ม.

ตัวอย่างที่ 2ต้องใช้ลวดนิเกิลขนาดเส้นผ่านศูนย์กลาง 0.5 มม. เท่าใดเพื่อสร้างรีโอสแตตที่มีความต้านทาน 40 โอห์ม

คำตอบ. ตามตาราง. 1 เรากำหนดความต้านทาน 1 ม. ของสายนี้: R = 2.12 โอห์ม: ดังนั้นในการสร้างรีโอสแตทที่มีความต้านทาน 40 โอห์ม คุณต้องใช้ลวดที่มีความยาว l = 40 / 2.12 = 18.9 ม.

ลองทำการคำนวณแบบเดียวกันโดยใช้สูตร เราพบพื้นที่หน้าตัดของเส้นลวด s = 0.78 • 0.52 = 0.195 mm2 และความยาวของลวดจะเป็น l = 0.195 * 40 / 0.42 = 18.6 ม.