ความแรงของสนามแม่เหล็ก แรงแม่เหล็ก

มีกระแสไฟฟ้ารอบเส้นลวดหรือขดลวดเสมอ สนามแม่เหล็ก… สนามแม่เหล็กของแม่เหล็กถาวรเกิดจากการเคลื่อนที่ของอิเล็กตรอนในวงโคจรของอะตอม

สนามแม่เหล็กมีลักษณะเฉพาะด้วยความแรงของมัน ความแรงของสนามแม่เหล็ก H มีค่าใกล้เคียงกับความแข็งแรงเชิงกล เป็นปริมาณเวกเตอร์ กล่าวคือ มีขนาดและทิศทาง

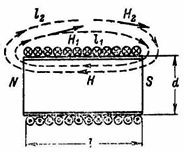
สนามแม่เหล็ก ซึ่งก็คือพื้นที่รอบๆ แม่เหล็กสามารถแสดงเป็นเส้นที่เต็มไปด้วยแม่เหล็ก ซึ่งถือว่าออกจากขั้วเหนือของแม่เหล็กและเข้าสู่ขั้วใต้ (รูปที่ 1) เส้นสัมผัสกับเส้นแม่เหล็กระบุทิศทางของความแรงของสนามแม่เหล็ก

สนามแม่เหล็กจะแรงกว่าเมื่อเส้นแม่เหล็กหนาแน่นกว่า (ที่ขั้วของแม่เหล็กหรือภายในขดลวดที่มีกระแสไฟฟ้า)

ยิ่งกระแส I และจำนวนรอบของขดลวด ω มากเท่าไร สนามแม่เหล็กที่อยู่ใกล้เส้นลวดก็ยิ่งมากขึ้น (หรือภายในขดลวด)

ความแรงของสนามแม่เหล็ก H ณ จุดใด ๆ ในอวกาศจะยิ่งมากขึ้น ผลคูณ ∙ ω ก็ยิ่งมากขึ้นเท่านั้น และความยาวของเส้นแม่เหล็กก็จะยิ่งสั้นลง:

H = (ฉัน ∙ ω) / ล.

จากสมการที่ว่าหน่วยวัดความแรงของสนามแม่เหล็กคือแอมแปร์ต่อเมตร (A / m)

สำหรับเส้นแม่เหล็กแต่ละเส้นในสนามสม่ำเสมอที่กำหนด ผลิตภัณฑ์ H1 ∙ l1 = H2 ∙ l2 = … = H ∙ l = I ∙ ω เท่ากัน (รูปที่ 1)

ข้าว. 1.

ผลิตภัณฑ์ H ∙ l ในวงจรแม่เหล็กจะคล้ายกับแรงดันไฟฟ้าในวงจรไฟฟ้า และเรียกว่า แรงดันแม่เหล็ก และนำมาตลอดความยาวของเส้นเหนี่ยวนำแม่เหล็กเรียกว่า แรงแม่เหล็ก (ns) Fm: Fm = H ∙ l = ฉัน ∙ ω

แรงแม่เหล็ก Fm วัดเป็นแอมแปร์ แต่ในทางปฏิบัติทางเทคนิค แทนที่จะใช้ชื่อแอมแปร์ จะใช้ชื่อแอมแปร์-เทิร์น ซึ่งเน้นว่า Fm เป็นสัดส่วนกับกระแสและจำนวนรอบ

สำหรับขดลวดทรงกระบอกที่ไม่มีแกนซึ่งมีความยาวมากกว่าเส้นผ่านศูนย์กลาง (l≫d) มาก สนามแม่เหล็กภายในขดลวดสามารถพิจารณาได้เหมือนกัน เช่น ด้วยความแรงของสนามแม่เหล็ก H เท่ากันในพื้นที่ภายในทั้งหมดของขดลวด (รูปที่ 1) เนื่องจากสนามแม่เหล็กภายนอกขดลวดดังกล่าวอ่อนแอกว่าภายในมาก จึงละเลยสนามแม่เหล็กภายนอกได้ และในการคำนวณจะถือว่า n ขดลวด c เท่ากับผลคูณของความแรงของสนามภายในขดลวดคูณความยาวของขดลวด

ขั้วของสนามแม่เหล็กของเส้นลวดและขดลวดปัจจุบันถูกกำหนดโดยกฎ gimbal หากการเคลื่อนที่ไปข้างหน้าของ gimbal สอดคล้องกับทิศทางของกระแส ทิศทางการหมุนของที่จับ gimbal จะระบุทิศทางของเส้นแม่เหล็ก

ตัวอย่างของ

1. กระแส 3 A ไหลผ่านขดลวด 2,000 รอบ n คืออะไร v. ขดลวด?

Fm = I ∙ ω = 3 ∙ 2000 = 6000 A แรงแม่เหล็กของขดลวดคือ 6000 แอมแปร์-เทิร์น

2. ขดลวด 2,500 รอบควรมี n หน้า 10,000 A. กระแสอะไรที่ต้องไหลผ่าน?

ฉัน = Fm / ω = (ฉัน ∙ ω) / ω = 10,000/2500 = 4 A.

3.กระแส I = 2 A ไหลผ่านขดลวด ขดลวดต้องมีกี่รอบจึงจะให้ n หมู่บ้าน 8000 เอ?

ω = Fm / I = (I ∙ ω) / I = 8000/2 = 4000 รอบ

4. ภายในขดลวดยาว 10 ซม. มี 100 รอบ จำเป็นต้องให้ความแรงของสนามแม่เหล็ก H = 4,000 A / m ขดลวดควรรับกระแสเท่าใด

แรงแม่เหล็กของขดลวดคือ Fm = H ∙ l = I ∙ ω ดังนั้น 4000 A / m ∙ 0.1 m = I ∙ 100; ฉัน = 400/100 = 4 ก.

5. เส้นผ่านศูนย์กลางของขดลวด (โซลินอยด์) คือ D = 20 มม. และความยาวของมันคือ l = 10 ซม. ขดลวดนั้นพันจากลวดทองแดงที่มีเส้นผ่านศูนย์กลาง d = 0.4 มม. ความแรงของสนามแม่เหล็กภายในคอยล์เป็นเท่าใดหากเปิดสวิตช์ที่ 4.5V?

จำนวนรอบโดยไม่คำนึงถึงความหนาของฉนวน ω = l∶d = 100∶0.4 = 250 รอบ

ความยาวห่วง π ∙ d = 3.14 ∙ 0.02 ม. = 0.0628 ม.

ความยาวคอยล์ l1 = 250 ∙ 0.0628 ม. = 15.7 ม.

ความต้านทานที่ใช้งานของขดลวด r = ρ ∙ l1 / S = 0.0175 ∙ (4 ∙ 15.7) / (3.14 ∙ 0.16) = 2.2 โอห์ม

ปัจจุบัน I = U / r = 4.5 / 2.2 = 2.045 A ≈2 A.

ความแรงของสนามแม่เหล็กภายในขดลวด H = (I ∙ ω) / l = (2 ∙ 250) / 0.1 = 5,000 A / m.

6. กำหนดความแรงของสนามแม่เหล็กที่ระยะ 1, 2, 5 ซม. จากเส้นตรงที่กระแส I = 100 A ไหลผ่าน

ลองใช้สูตร H ∙ l = I ∙ ω

สำหรับลวดตรง ω = 1 และ l = 2 ∙ π ∙ r

โดยที่ H = I / (2 ∙ π ∙ r)

H1 = 100 / (2 ∙ 3.14 ∙ 0.01) = 1590 A / m; H2 = 795 A/m; H3 = 318 A/ม.