วงจรไฟฟ้าเชิงเส้นแบบไม่แบรนช์และแบรนช์ที่มีแหล่งจ่ายเดียว

หากมีองค์ประกอบแฝงจำนวนมากพร้อมกับแหล่งที่มาของ e เป็นต้น ค. สร้างวงจรไฟฟ้า การเชื่อมต่อโครงข่ายสามารถทำได้หลายวิธี มีโครงร่างทั่วไปต่อไปนี้สำหรับการเชื่อมต่อดังกล่าว

การเชื่อมต่อแบบอนุกรมขององค์ประกอบ นี่คือการเชื่อมต่อที่ง่ายที่สุด ด้วยการเชื่อมต่อนี้กระแสเดียวกันจะไหลในองค์ประกอบทั้งหมดของวงจร ตามรูปแบบนี้สามารถเชื่อมต่อองค์ประกอบแบบพาสซีฟทั้งหมดของวงจรได้จากนั้นวงจรจะเป็นวงจรเดียวที่ไม่ได้แยกสาขา (รูปที่ 1., a) หรือเพียงบางส่วนขององค์ประกอบของวงจรหลายวงจรเท่านั้น เชื่อมต่อ

หากองค์ประกอบ n ชิ้นเชื่อมต่อแบบอนุกรมซึ่งกระแส I เดียวกันไหล แรงดันไฟฟ้าที่ขั้วของวงจรจะเท่ากับผลรวมของแรงดันตกในองค์ประกอบ n ชิ้นที่เชื่อมต่อแบบอนุกรม เช่น

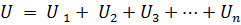
หรือ:

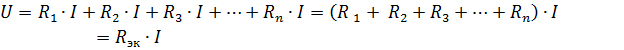
โดยที่ Rek คือความต้านทานของวงจรสมมูล

ดังนั้น ความต้านทานสมมูลขององค์ประกอบแบบพาสซีฟที่เชื่อมต่อเป็นอนุกรมจึงเท่ากับผลรวมของความต้านทานขององค์ประกอบเหล่านี้... โครงร่างไฟฟ้า (รูปที่1, a) สามารถแสดงวงจรสมมูลได้ (รูปที่ 1, b) ประกอบด้วยองค์ประกอบหนึ่งที่มีความต้านทานเท่ากัน Rek

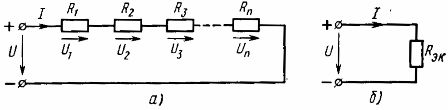
ข้าว. 1. แผนภาพการเชื่อมต่อแบบอนุกรมขององค์ประกอบเชิงเส้น (a) และโครงร่างที่เทียบเท่า (b)

เมื่อคำนวณวงจรที่มีองค์ประกอบเชื่อมต่อเป็นอนุกรมที่แรงดันไฟฟ้าที่กำหนดของแหล่งพลังงานและความต้านทานขององค์ประกอบ กระแสในวงจรจะคำนวณตามกฎของโอห์ม:

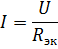
แรงดันตกคร่อมองค์ประกอบ kth

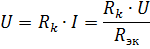
ขึ้นอยู่กับความต้านทานขององค์ประกอบนี้เท่านั้น แต่ยังขึ้นอยู่กับความต้านทานที่เทียบเท่า Rek นั่นคือความต้านทานขององค์ประกอบอื่น ๆ ของวงจร นี่เป็นข้อเสียที่สำคัญของการเชื่อมต่อองค์ประกอบแบบอนุกรม ในกรณีที่จำกัด เมื่อความต้านทานขององค์ประกอบใด ๆ ของวงจรมีค่าเท่ากับอนันต์ (วงจรเปิด) กระแสในองค์ประกอบทั้งหมดของวงจรจะกลายเป็นศูนย์

เนื่องจากเมื่อเชื่อมต่อแบบอนุกรมกระแสในองค์ประกอบทั้งหมดของวงจรจะเท่ากันอัตราส่วนของแรงดันตกในองค์ประกอบจะเท่ากับอัตราส่วนของความต้านทานขององค์ประกอบเหล่านี้:

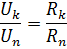
การเชื่อมต่อแบบขนานขององค์ประกอบ - นี่คือการเชื่อมต่อที่ใช้แรงดันไฟฟ้าเดียวกันกับองค์ประกอบทั้งหมดของวงจร ตามรูปแบบการเชื่อมต่อแบบขนานสามารถเชื่อมต่อองค์ประกอบแบบพาสซีฟทั้งหมดของวงจร (รูปที่ 2, a) หรือเพียงบางส่วนเท่านั้น แต่ละองค์ประกอบที่เชื่อมต่อแบบขนานจะสร้างสาขาแยกจากกัน ดังนั้นวงจรที่มีการเชื่อมต่อแบบขนานขององค์ประกอบที่แสดงในรูปที่ 2, a แม้ว่าจะเป็นวงจรง่าย ๆ (เนื่องจากมีเพียงสองโหนด) แต่ก็มีการแตกแขนงในเวลาเดียวกัน

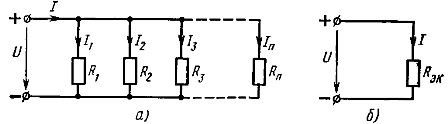
ข้าว. 2. รูปแบบการเชื่อมต่อแบบขนานขององค์ประกอบเชิงเส้น (a) และรูปแบบที่เทียบเท่า (b)

ในแต่ละสาขาคู่ขนานปัจจุบัน

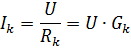
โดยที่ Gk คือค่าการนำไฟฟ้าของสาขาที่ k

จาก กฎข้อที่หนึ่งของ Kirchhoff

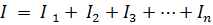
หรือ

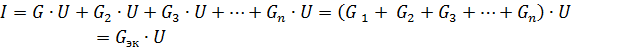
โดยที่ Gec คือค่าการนำไฟฟ้าของวงจรสมมูล

ดังนั้น เมื่อองค์ประกอบแบบพาสซีฟเชื่อมต่อแบบขนาน ค่าการนำไฟฟ้าที่เท่ากันจะเท่ากับผลรวมของค่าการนำไฟฟ้าขององค์ประกอบเหล่านี้... ค่าการนำไฟฟ้าที่สมมูลกันจะมากกว่าค่าการนำไฟฟ้าของส่วนใดส่วนหนึ่งของสาขาคู่ขนานเสมอ ค่าการนำไฟฟ้าสมมูล GEK สอดคล้องกับความต้านทานเทียบเท่า Rek = 1 / Gek

จากนั้นวงจรสมมูลที่แสดงในรูป 2, a, จะมีรูปแบบดังรูปที่. 2, b. กระแสในส่วนที่ไม่ได้แยกส่วนของวงจรที่มีการเชื่อมต่อแบบขนานขององค์ประกอบสามารถกำหนดได้จากวงจรนี้ตามกฎของโอห์ม:

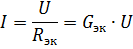
ดังนั้นหากแรงดันไฟฟ้าคงที่ด้วยจำนวนองค์ประกอบที่เชื่อมต่อแบบขนานเพิ่มขึ้น (ซึ่งนำไปสู่การเพิ่มค่าการนำไฟฟ้าที่เท่ากัน) กระแสในส่วนที่ไม่แตกแขนงของวงจร (กระแสไฟ) จะเพิ่มขึ้น

จากสูตร

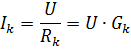
จะเห็นได้ว่ากระแสไฟในแต่ละสาขาขึ้นอยู่กับค่า conductance ของสาขานั้นเท่านั้น ไม่ได้ขึ้นกับ conductance ของสาขาอื่น ความเป็นอิสระของโหมดสาขาคู่ขนานจากกันและกันเป็นข้อได้เปรียบที่สำคัญของการเชื่อมต่อแบบขนานขององค์ประกอบแบบพาสซีฟ ในการติดตั้งทางอุตสาหกรรม ในกรณีส่วนใหญ่จะใช้การเชื่อมต่อแบบขนานของตัวรับไฟฟ้า ตัวอย่างที่เห็นได้ชัดเจน คือ การรวมหลอดไฟฟ้าเพื่อให้แสงสว่าง

เนื่องจากในการเชื่อมต่อแบบขนานจะใช้แรงดันไฟฟ้าเดียวกันกับองค์ประกอบทั้งหมดและกระแสในแต่ละสาขาจะเป็นสัดส่วนกับสื่อนำไฟฟ้าของสาขานั้น อัตราส่วนของกระแสในสาขาขนานจะเท่ากับอัตราส่วนของสื่อนำไฟฟ้าของสาขาเหล่านี้หรือสัดส่วนผกผัน ต่ออัตราส่วนของความต้านทาน:

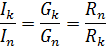
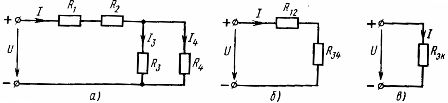
การเชื่อมต่อองค์ประกอบแบบผสมคือการรวมกันของการเชื่อมต่อแบบอนุกรมและแบบขนาน ห่วงโซ่ดังกล่าวสามารถมีจำนวนโหนดและสาขาที่แตกต่างกัน ตัวอย่างของการเชื่อมต่อแบบผสมแสดงในแผนภาพ (รูปที่ 3, a)

ข้าว. 3. โครงร่างการเชื่อมต่อแบบผสมขององค์ประกอบเชิงเส้น (a) และโครงร่างที่เทียบเท่า (b, c)

ในการคำนวณวงจรดังกล่าวจำเป็นต้องกำหนดความต้านทานที่เท่ากันอย่างต่อเนื่องสำหรับส่วนต่าง ๆ ของวงจรที่เป็นการเชื่อมต่อแบบอนุกรมหรือแบบขนานเท่านั้น ในวงจรที่พิจารณามีการเชื่อมต่อแบบอนุกรมขององค์ประกอบที่มีความต้านทาน R1 และ R2 และการเชื่อมต่อแบบขนานขององค์ประกอบที่มีความต้านทาน R3 และ R4 การใช้ความสัมพันธ์ที่ได้รับก่อนหน้านี้ระหว่างพารามิเตอร์ขององค์ประกอบวงจรกับอนุกรมและการเชื่อมต่อแบบขนาน วงจรไฟฟ้าจริงสามารถถูกแทนที่ด้วยวงจรสมมูลได้อย่างต่อเนื่อง

ความต้านทานที่เท่ากันขององค์ประกอบที่ต่ออนุกรมกัน

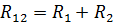
ความต้านทานที่เท่ากันขององค์ประกอบที่เชื่อมต่อแบบขนาน R3 และ R4

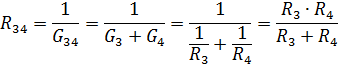
วงจรสมมูลที่มีความต้านทานขององค์ประกอบ R12 และ R34 แสดงในรูปที่ 3, ข. สำหรับการเชื่อมต่ออนุกรมของ R12 และ R34 ความต้านทานเทียบเท่าคือ

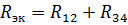
และวงจรสมมูลที่เกี่ยวข้องแสดงในรูปที่ 2, ข. มาหากระแสในวงจรนี้กัน:

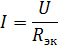
นี่คือกระแสจ่ายและกระแสในองค์ประกอบ R1 และ R2 ของวงจรจริงในการคำนวณกระแส I3 และ I4 ให้กำหนดแรงดันไฟฟ้าในส่วนของวงจรที่มีความต้านทาน R34 (รูปที่ 3, b):

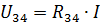
จากนั้นจะพบกระแส I3 และ I4 ตามกฎของโอห์ม:

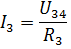
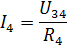
ในทำนองเดียวกัน คุณสามารถคำนวณวงจรไฟฟ้าอื่นๆ จำนวนหนึ่งที่มีการเชื่อมต่อแบบผสมขององค์ประกอบแบบพาสซีฟ

สำหรับวงจรซับซ้อนที่มีวงจรจำนวนมากและแหล่งกำเนิดของ e เป็นต้น c. การแปลงที่เทียบเท่ากันนั้นไม่สามารถทำได้เสมอไป คำนวณด้วยวิธีอื่น