การคำนวณโพเทนชิออมิเตอร์และการแบ่งแบบผสม

แนวคิดและสูตร

โพเทนชิออมิเตอร์คือความต้านทานแบบแปรผันที่มีแถบเลื่อนซึ่งรวมอยู่ในรูปที่

สำหรับรายละเอียดเพิ่มเติมดูที่ — โพเทนชิออมิเตอร์และการใช้งาน

แรงดันไฟฟ้า U ใช้กับจุดที่ 1 และ 2 แรงดันไฟฟ้าที่ปรับได้จะถูกลบออกจากจุดที่ 2 และ 3 ซึ่งมีค่าน้อยกว่า U และขึ้นอยู่กับตำแหน่งของแถบเลื่อน ตัวแบ่งแรงดันไฟฟ้ามีรูปแบบที่คล้ายกัน แต่ไม่สามารถปรับได้และไม่มีตัวเลื่อนแบบเคลื่อนย้ายได้

โพเทนชิโอมิเตอร์ ตัวแบ่งแรงดัน และการแบ่งที่ซับซ้อนคำนวณโดยใช้ กฎของเคอร์ชอฟฟ์เช่นการคำนวณวงจรธรรมดาที่มีความต้านทาน

ตัวอย่างของ

1. แรงดันแหล่งกำเนิดคือ U = 24 V ความต้านทานรวมของโพเทนชิออมิเตอร์คือ r = 300 โอห์ม มอเตอร์ติดตั้งแยกต่างหากเพื่อให้ r1 = 50 โอห์ม แรงดันไฟฟ้า U1 ใดที่สามารถลบออกจากจุดที่ 3 และ 2 (รูปที่ 1)

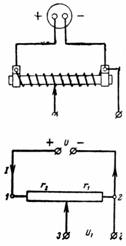
ข้าว. 1.

กระแส I และแรงดัน U คร่อมความต้านทาน r สัมพันธ์กันโดยสูตร I ∙ r = U

ตัวเลื่อนโพเทนชิออมิเตอร์จะแยกความต้านทานบางส่วนออกไป เช่น ความต้านทาน r1 แรงดันไฟตกระหว่างจุด 3 และ 2 เท่ากับ I ∙ r1 = U1

จากอัตราส่วนของแรงดันตกเราได้รับความเท่าเทียมกัน (I ∙ r1) / (I ∙ r) = U1 / U ยิ่งความต้านทาน r1 ยิ่งมาก ค่าของแรงดัน U1 ระหว่างจุดที่ 3 และ 2 จะยิ่งมากขึ้น U1 = r1 / r ∙ U = 50/300 ∙ 24 = 4 V.

2. โหลดโพเทนชิออมิเตอร์ (รูปที่ 2) บนหลอดไฟที่มีความต้านทาน r = 100 โอห์ม โพเทนชิออมิเตอร์ถูกแบ่งโดยแถบเลื่อนออกเป็นสองส่วนโดย r1 = 600 โอห์ม และ r2 = 200 โอห์ม กำหนดแรงดัน Ul และกระแสไฟ Il

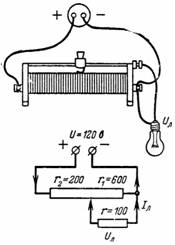
ข้าว. 2.

กระแส I ไหลผ่านความต้านทาน r2 และกระแส Il ไหลผ่านหลอดไฟ กระแส I-Il ไหลผ่านความต้านทาน r1 ซึ่งสร้างแรงดันไฟฟ้าคร่อมความต้านทาน r1 เท่ากับแรงดันไฟฟ้าของหลอดไฟ: (I-Il) ∙ r1 = Ul

ในทางกลับกัน แรงดันไฟจะเท่ากับแรงดันไฟต้นทางลบ แรงดันตก ที่แนวต้าน r2: U-I ∙ r2 = Ul

กระแส I เท่ากับแรงดันแหล่งจ่ายหารด้วยความต้านทานผลลัพธ์ของการเชื่อมต่อแบบอนุกรมขนานของตัวต้านทาน:

ฉัน = U / (r2 + (r ∙ r1) / (r + r1)).

เราแทนที่นิพจน์สำหรับกระแสรวมของแหล่งที่มาในสมการที่สอง:

U-U / (r2 + (r ∙ r1) / (r + r1)) ∙ r2 = Ul

หลังจากการเปลี่ยนแปลง เราได้รับนิพจน์สำหรับแรงดันไฟฟ้าของหลอดไฟ:

Ul = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r) ∙ r

หากเราแปลงนิพจน์นี้โดยเริ่มจากข้อเท็จจริงที่ว่า Ul = Il ∙ r เราจะได้นิพจน์สำหรับกระแสไฟ:

อิล = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r).

แทนค่าตัวเลขลงในสมการผลลัพธ์:

Ul = (120 ∙ 600) / (600 ∙ 200 + 600 ∙ 100 + 200 ∙ 100) ∙ 100 = 7200000/200000 = 36 V;

อิล = Ul / r = 36/100 = 0.36 ก.

3. คำนวณแรงดันไฟฟ้าขึ้นและ Ip ปัจจุบันของอุปกรณ์วัดที่เชื่อมต่อกับส่วนของโพเทนชิออมิเตอร์ อุปกรณ์มีความต้านทาน r = 1,000 โอห์ม จุดแยกจะแบ่งความต้านทานของตัวแบ่งออกเป็น r2 = 500 โอห์ม และ r1 = 7000 โอห์ม (รูปที่ 3)แรงดันไฟฟ้าที่ขั้วของโพเทนชิออมิเตอร์ U = 220 V.

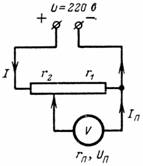
ข้าว. 3.

เมื่อใช้สูตรที่ได้รับก่อนหน้านี้ เราสามารถเขียนได้ว่ากระแสที่ไหลผ่านอุปกรณ์คือ:

ใน = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r) = (220 ∙ 7000) / (7000 ∙ 500 + 7000 ∙ 1,000 + 500 ∙ 1,000)= 1540000/11000000 = 1.54 / 11 = 0.14 ก.

ขึ้น = Ip ∙ r = 0.14 ∙ 1,000 = 14 V.

4. คำนวณแรงดันไฟฟ้าของอุปกรณ์ขึ้นหากใช้กระแส Ip = 20 mA และเชื่อมต่อกับโพเทนชิออมิเตอร์โดยแบ่งเป็นความต้านทาน r2 = 10 ^ 4 Ohm และ r1 = 2 ∙ 10 ^ 4 Ohm (รูปที่ 3)

แรงดันรวมในตัวแบ่งแรงดันเท่ากับผลรวมของแรงดันตกในส่วนต่าง ๆ (ผ่านความต้านทาน r1 และ r2): U = I ∙ r2 + I1 ∙ r1; U = I ∙ r2 + ขึ้น

กระแสไฟแยกจากจุดสัมผัสมอเตอร์: I = I1 + Ip; I = Upn / r1 + In

เราแทนค่าของกระแส I ลงในสมการแรงดันไฟฟ้า:

U = (Un / r1 + In) ∙ r2 + Un;

U = Uп / r1 ∙ r2 + Iп ∙ r2 + Uп;

U = Upn ∙ (r2 / r1 +1) + In ∙ r2

ดังนั้น แรงดันไฟฟ้าของอุปกรณ์ Upn = (U-In ∙ r2) / (r1 + r2) ∙ r1

แทนค่าตัวเลข: Up = (220-0.02 ∙ 10000) / 30000 ∙ 20000 = 20/3 ∙ 2 = 13.3 V.

5. แหล่งกำเนิดไฟฟ้ากระแสตรงที่มีแรงดันไฟฟ้า U = 120 V จ่ายวงจรแอโนดของเครื่องรับวิทยุผ่านโพเทนชิออมิเตอร์ (ตัวแบ่งแรงดัน) ซึ่งมีความต้านทาน r = 10,000 โอห์มร่วมกับตัวกรอง แรงดันไฟฟ้า U1 จะถูกลบออกโดยความต้านทาน r2 = 8000 โอห์ม คำนวณแรงดันแอโนดที่ไม่มีโหลดและที่กระแสโหลด I = 0.02 A (รูปที่ 4)

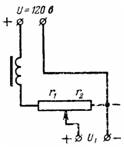
ข้าว. 4.

กรณีแรกคล้ายกับตัวอย่างที่ 1:

U: U1 = r: r2;

U1 = r2 / r ∙ U = 8000/10000 ∙ 120 = 96 V.

กรณีที่สองคล้ายกับตัวอย่างที่ 3:

U1 = (U-I ∙ r1) / r ∙ r2;

U1 = (120-0.02 ∙ 2000) / 10,000 ∙ 8000 = 64 V.

เมื่อทำการชาร์จ แรงดันไฟจะลดลงจาก 96 เป็น 64 Vหากต้องการแรงดันไฟฟ้ามากขึ้นควรเลื่อนแถบเลื่อนไปทางซ้ายนั่นคือควรเพิ่มความต้านทาน r2

6. แรงดันไฟฟ้า Ua และ Ub จะถูกลบออกโดยตัวแบ่งแรงดันไฟฟ้า ความต้านทานรวมของตัวแบ่งแรงดันที่เชื่อมต่อกับแรงดัน U1 = 220 V คือ r = 20,000 โอห์ม แรงดันไฟฟ้า Ua ในความต้านทาน r3 = 12,000 โอห์มที่มีการใช้กระแสไฟฟ้า Ia = 0.01 A และแรงดันไฟฟ้า Ub ในความต้านทาน r2 + r3 = 18,000 โอห์มที่มีการใช้กระแสไฟฟ้า Ib = 0.02 A (รูปที่ 5)

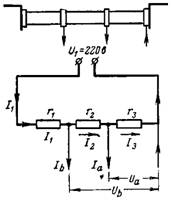
ข้าว. 5.

ความต้านทานแรงดันไฟฟ้า r3

เอื้อ = I3 ∙ r3;

เอื้อ = (U -Ia ∙ (r1 + r2) -Ib ∙ r1) / r ∙ r3;

Ua = (220-0.01 ∙ 8000-0.02 ∙ 2000) / 20 000 ∙ 12000 = (220-80-40) / 20 ∙ 12 = 60 V.

แรงดัน Ub เท่ากับผลรวมของแรงดันตกคร่อม Ua ที่ตกคร่อมความต้านทาน r3 และแรงดันตกคร่อมความต้านทาน r2 แรงดันตกคร่อมความต้านทาน r2 เท่ากับ I2 ∙ r2 I2 ปัจจุบัน = Ia + I3 I3 ปัจจุบันสามารถคำนวณได้ตามตัวอย่างที่ 1:

I3 = (220-80-40) / 20,000 = 0.005 A;

I2 = Ia + I3 = 0.01 + 0.005 = 0.015 ก.

แรงดันไฟฟ้า Ub = Ua + I2 ∙ r2 = 5 + 0.015 ∙ 6000 = 150 V.

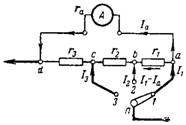
7. คำนวณการแบ่งรวมสำหรับมิลลิแอมป์มิเตอร์เพื่อให้ตำแหน่งต่างๆ ของสวิตช์มีช่วงการวัดต่อไปนี้: I1 = 10 mA; I2 = 30mA; I3 = 100mA. แผนภาพการเชื่อมต่อ shunt แสดงในรูปที่ 6. ความต้านทานภายในของอุปกรณ์ ra = 40 โอห์ม ช่วงการวัดที่แท้จริงของมิลลิแอมป์มิเตอร์ 2 มิลลิแอมป์

ข้าว. 6.

เมื่อทำการวัดกระแส I≤2mA การปัดจะปิด

ก) เมื่อวัดกระแส I = 10 mA สวิตช์จะอยู่ในตำแหน่ง 1 และกระแส 10-2 = 8 mA จะไหลผ่านความต้านทานการปัดทั้งหมด แรงดันตกคร่อมความต้านทานการแบ่ง Ush และอุปกรณ์ Ua ระหว่างจุด d และ a ต้องเท่ากัน

อุช = เอื้อ;

(I1-Ia) ∙ (r1 + r2 + r3) = Ia ∙ รา;

0.008 ∙ (r1 + r2 + r3) = 0.002 ∙ 40

b) เมื่อวัดกระแส I2 = 30 mA สวิตช์อยู่ในตำแหน่ง 2 กระแสที่วัดได้จะแบ่งที่จุด b เมื่อตัวชี้อุปกรณ์โก่งเต็มที่ กระแส Ia = 2 mA จะผ่านความต้านทาน r1 และอุปกรณ์ ra

ส่วนที่เหลือของ I2-Ia ปัจจุบันจะผ่านความต้านทาน r2 และ r3 กระแสจะสร้างแรงดันตกคร่อมทั้งสองกิ่งระหว่างจุด d และ b:

(I2-Ia) ∙ (r2 + r3) = Ia ∙ r1 + Ia ∙ รา;

(0.03-0.002) ∙ (r2 + r3) = 0.002 ∙ (r1 + 40)

ค) ในทำนองเดียวกัน เราจะทำการคำนวณเมื่อเพิ่มช่วงการวัดเป็น I3 = 100 mA กระแส I3-Ia จะไหลผ่านแนวต้าน r3 และกระแส Ia ผ่านแนวต้าน r1, r2, ra แรงดันไฟฟ้าในทั้งสองสาขาเท่ากัน: (I3-Ia) ∙ r3 = Ia ∙ r1 + Ia ∙ r2 + Ia ∙ ra;

0.098 ∙ r3 = 0.002 ∙ (r1 + r2 + 40)

เราได้สามสมการที่มีค่าความต้านทานสามค่าที่ไม่รู้จัก r1, r2 และ r3

เราคูณสมการทั้งหมดด้วย 1,000 แล้วแปลงสมการ:

r1 + r2 + r3 = 10;

14 ∙ (r2 + r3) -r1 = 40;

49 ∙ r3-r1-r2 = 40.

เพิ่มสมการที่หนึ่งและสาม: 50 ∙ r3 = 50;

r3 = 50/50 = 1 โอห์ม

เพิ่มสมการที่หนึ่งและสอง: 15 ∙ r2 + 15 ∙ r3 = 50;

15 ∙ r2 + 15 ∙ 1 = 50;

15 ∙ r2 = 35; r2 = 2.34 โอห์ม

ลองแทนผลลัพธ์ที่ได้ในสมการแรก: r1 + 35/15 + 1 = 10;

15 ∙ r1 + 35 + 15 = 150;

r1 = 100/15 = 6.66 โอห์ม

สามารถตรวจสอบความถูกต้องของการคำนวณได้โดยการแทนค่าความต้านทานที่ได้ลงในสมการ