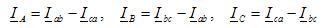การคำนวณวงจรสามเฟส

โซ่ กระแสสลับสามเฟส ประกอบด้วยแหล่งจ่ายไฟสามเฟส ผู้บริโภคสามเฟส และสายสื่อสารที่เชื่อมต่อระหว่างกัน

แหล่งจ่ายไฟแบบสามเฟสแบบสมมาตรสามารถแสดงเป็นแหล่งจ่ายไฟแบบเฟสเดียวสามตัวที่ทำงานที่ความถี่เดียวกันด้วยแรงดันไฟฟ้าเดียวกันและมีมุมเฟสในเวลา 120 ° แหล่งที่มาเหล่านี้สามารถเชื่อมต่อแบบสตาร์หรือเดลต้าได้

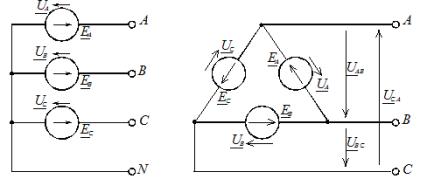
เมื่อเชื่อมต่อในดาวฤกษ์ จุดเริ่มต้นตามเงื่อนไขของเฟสจะใช้ในการเชื่อมต่อตัวนำเชิงเส้นสามตัว A, B, C และจุดสิ้นสุดของเฟสจะรวมกันที่จุดเดียว ซึ่งเรียกว่าจุดกลางของแหล่งพลังงาน (เครื่องกำเนิดไฟฟ้าสามเฟส หรือหม้อแปลง) จุดนี้สามารถเชื่อมต่อสายกลาง N ได้ แผนภาพการเชื่อมต่อแบบดาวของแหล่งพลังงานแสดงในรูปที่ 1, a

ข้าว. 1. ไดอะแกรมการเชื่อมต่อของเฟสแหล่งจ่ายไฟ: a — star; ข — สามเหลี่ยม

แรงดันไฟฟ้าระหว่างสายและตัวนำที่เป็นกลางเรียกว่าเฟส และระหว่างสายตัวนำเรียกว่า เส้น (สำหรับรายละเอียดเพิ่มเติม ดูที่นี่ – แรงดันไฟฟ้าของสายและเฟส).

วี แบบฟอร์มบูรณาการ รายการนิพจน์สำหรับแรงดันเฟสคือ:

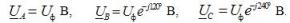
แรงดันไฟฟ้าของสายที่สอดคล้องกันเมื่อเชื่อมต่อกับดาว:

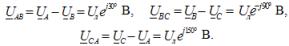
ที่นี่ Uf คือโมดูลัสแรงดันเฟสของแหล่งพลังงานและ Ul คือโมดูลัสแรงดันสาย ในระบบสามเฟสแบบสมมาตร เมื่อเฟสของแหล่งกำเนิดเชื่อมต่อกับดาว มีความสัมพันธ์ระหว่างแรงดันไฟฟ้าเหล่านี้:

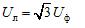
เมื่อเชื่อมต่อเฟสด้วยรูปสามเหลี่ยม อุปกรณ์จ่ายไฟของเฟสจะเชื่อมต่อเป็นอนุกรมในวงจรปิด (รูปที่ 1, b)

สายเส้นตรงสามเส้น A, B, C ถูกดึงออกมาจากจุดที่รวมแหล่งที่มาเข้าด้วยกันไปที่โหลด จากรูปที่ 1, b จะเห็นได้ว่าเอาต์พุตของแหล่งเฟสเชื่อมต่อกับสายเชิงเส้น ดังนั้นเมื่อเฟสของแหล่งสัญญาณเชื่อมต่อกันด้วยรูปสามเหลี่ยม แรงดันเฟสจะเท่ากับเชิงเส้น ในกรณีนี้ไม่มีลวดที่เป็นกลาง

โหลดสามารถเชื่อมต่อกับแหล่งจ่ายไฟสามเฟส ในแง่ของขนาดและลักษณะ โหลดสามเฟสสามารถสมมาตรและไม่สมมาตรได้

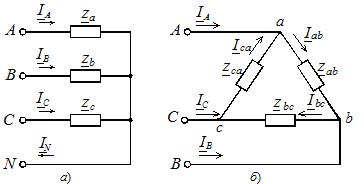
ในกรณีของโหลดแบบสมมาตร ความต้านทานที่ซับซ้อนของทั้งสามเฟสจะเท่ากัน และถ้าความต้านทานเหล่านี้แตกต่างกัน โหลดจะไม่สมดุล ขั้นตอนการโหลดสามารถเชื่อมต่อกันด้วยสตาร์หรือเดลต้า (รูปที่ 2) โดยไม่คำนึงถึงโครงร่างการเชื่อมต่อต้นทาง

ข้าว. 2. โหลดไดอะแกรมการเชื่อมต่อเฟส

การเชื่อมต่อแบบดาวอาจมีหรือไม่มีสายกลางก็ได้ (ดูรูปที่ 2, a) การไม่มีสายกลางช่วยลดการเชื่อมต่อที่เข้มงวดของแรงดันโหลดกับแรงดันแหล่งจ่าย และในกรณีของเฟสโหลดแบบไม่สมมาตร แรงดันเหล่านี้จะไม่เท่ากันเพื่อแยกความแตกต่าง เราตกลงที่จะใช้อักษรตัวพิมพ์ใหญ่ในดัชนีการกำหนดตัวอักษรของแรงดันและกระแสของแหล่งจ่าย และอักษรตัวพิมพ์เล็กในพารามิเตอร์เฉพาะโหลด

อัลกอริทึมสำหรับการวิเคราะห์วงจรสามเฟสขึ้นอยู่กับรูปแบบการเชื่อมต่อโหลด พารามิเตอร์เริ่มต้น และวัตถุประสงค์ของการคำนวณ

วิธีสองโหนดใช้ในการกำหนดแรงดันเฟสด้วยโหลดที่เชื่อมต่อกับดาวที่ไม่สมดุลโดยไม่มีตัวนำที่เป็นกลาง ตามวิธีนี้ การคำนวณเริ่มต้นด้วยการกำหนดแรงดันไฟฟ้า UN ระหว่างจุดที่เป็นกลางของแหล่งจ่ายและโหลด ซึ่งเรียกว่าแรงดันเบี่ยงเบนที่เป็นกลาง:

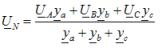
โดยที่ ya, yb, yc — ค่าที่อนุญาตของเฟสการโหลดที่สอดคล้องกันในรูปแบบที่ซับซ้อน

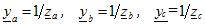
แรงดันไฟฟ้าข้ามเฟสของโหลดที่ไม่สมดุลพบได้จากนิพจน์:

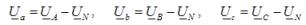
ในกรณีพิเศษของความไม่สมดุลของโหลด เมื่อในกรณีที่ไม่มีตัวนำที่เป็นกลาง การลัดวงจรเกิดขึ้นในเฟสหนึ่งของโหลด แรงดันไบอัสที่เป็นกลางจะเท่ากับแรงดันเฟสของแหล่งจ่ายของเฟสที่เกิดการลัดวงจร ที่เกิดขึ้น.

แรงดันไฟฟ้าในเฟสปิดของโหลดเป็นศูนย์และอีกสองตัวมีค่าเท่ากับแรงดันไฟฟ้าของสาย ตัวอย่างเช่น สมมติว่าเกิดการลัดวงจรในเฟส B แรงดันไบอัสที่เป็นกลางสำหรับกรณีนี้คือ UN = UB จากนั้นแรงดันเฟสของโหลด:

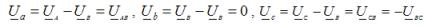
กระแสเฟสในโหลดยังเป็นกระแสตัวนำสำหรับโหลดประเภทใดก็ได้:

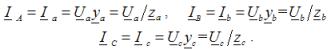
ในงานเมื่อคำนวณวงจรสามเฟสให้พิจารณาสามตัวเลือกสำหรับการเชื่อมต่อผู้บริโภคสามเฟสกับดาว: การเชื่อมต่อกับสายกลางต่อหน้าผู้บริโภคในสามเฟสการเชื่อมต่อกับสายกลางในกรณีที่ไม่มีผู้บริโภคในหนึ่งเดียว ของเฟสและการเชื่อมต่อโดยไม่มีสายกลางที่มีสารประกอบสั้นในเฟสโหลดใดเฟสหนึ่ง...

ในเวอร์ชันที่หนึ่งและสอง แรงดันเฟสที่สอดคล้องกันของแหล่งจ่ายจะอยู่ที่เฟสของโหลด และกระแสเฟสในโหลดจะถูกกำหนดโดยสูตรข้างต้น

ในรุ่นที่สาม แรงดันของเฟสโหลดไม่เท่ากับแรงดันเฟสของแหล่งจ่ายและถูกกำหนดโดยใช้การขึ้นต่อกัน

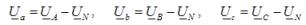
กระแสในสองเฟสที่ไม่ลัดวงจรถูกกำหนดตามกฎของโอห์ม โดยเป็นเศษส่วนของการแบ่งแรงดันเฟสโดยอิมพีแดนซ์ของเฟสนั้น ๆ กระแสลัดวงจรถูกกำหนดโดยใช้สมการตาม กฎข้อที่หนึ่งของ Kirchhoffรวบรวมสำหรับจุดที่เป็นกลางของโหลด

สำหรับตัวอย่างข้างต้นของการลัดวงจรเฟส B:

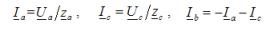
สำหรับโหลดแต่ละประเภท กำลังไฟฟ้าแบบแอกทีฟและรีแอกทีฟสามเฟสจะเท่ากับผลรวมของกำลังไฟฟ้าแอกทีฟและรีแอกทีฟของแต่ละเฟสตามลำดับ ในการกำหนดกำลังเฟสเหล่านี้ คุณสามารถใช้นิพจน์

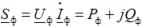
โดยที่ Uf,Azf คือความซับซ้อนของแรงดันและความซับซ้อนของกระแสคู่ในเฟสโหลด Pf, Qf — พลังงานที่ใช้งานและปฏิกิริยาในเฟสโหลด

กำลังไฟฟ้าสามเฟส: P = Pa + Pb + Pc

พลังงานปฏิกิริยาสามเฟส: Q = Qa + Qb + Vc

พลังงานปรากฏสามเฟส:

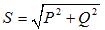
เมื่อเชื่อมต่อผู้บริโภคด้วยรูปสามเหลี่ยม วงจรจะใช้รูปแบบที่แสดงในรูปที่ 2, ข. ในโหมดนี้ การเชื่อมต่อเฟสของแหล่งจ่ายไฟแบบบาลานซ์จะไม่เกี่ยวข้อง

ตรวจพบแรงดันไฟฟ้าระหว่างสายจ่ายไฟในเฟสโหลด กระแสเฟสในโหลดถูกกำหนดโดยใช้ กฎของโอห์มสำหรับส่วนของวงจรAzf = Uf /zf โดยที่ Uf — แรงดันเฟสในโหลด (ตรงกับแรงดันไฟเมนของแหล่งพลังงาน) zf คือความต้านทานรวมของเฟสที่สอดคล้องกันของโหลด

กระแสในตัวนำเชิงเส้นถูกกำหนดโดยกระแสเฟสตามกฎข้อที่หนึ่งของ Kirchhoff สำหรับแต่ละโหนด (จุด a, b, c) ของวงจรที่แสดงในรูปที่ 2, b: