ทฤษฎีออโตมาตา ไฟไนต์ออโตมาตา

โครงสร้าง การออกแบบ หลักการทำงานของเครื่องจักรต่าง ๆ นั้นถูกกำหนดโดยวัตถุประสงค์การทำงานเป็นส่วนใหญ่ แยกแยะความแตกต่างระหว่างเทคโนโลยี การขนส่ง คอมพิวเตอร์ การทหาร และเครื่องจักรอื่นๆ คอมเพล็กซ์อัตโนมัติทั้งหมดที่ออกแบบมาเพื่อดำเนินกระบวนการทางเทคโนโลยีที่ซับซ้อนถูกนำมาใช้อย่างแพร่หลายในอุตสาหกรรมต่างๆ ออโตมาตาได้รับการออกแบบและสร้างขึ้นเพื่อทำหน้าที่ลอจิคัลต่างๆ (โลจิคัลแมชชีน)

ทฤษฎีออโตมาตา — ส่วนไซเบอร์เนติกส์ซึ่งเกิดขึ้นภายใต้อิทธิพลของข้อกำหนดของเทคโนโลยีคอมพิวเตอร์ดิจิทัลและเครื่องควบคุม ออโตมาตาแบบไม่ต่อเนื่องที่ศึกษาในทฤษฎีออโตมาตาคือแบบจำลองเชิงนามธรรมของระบบจริง (ทั้งทางเทคนิคและชีวภาพ) ที่ประมวลผลข้อมูลแบบไม่ต่อเนื่อง (ดิจิทัล) ตามขั้นตอนของเวลาที่ไม่ต่อเนื่อง

ทฤษฎีออโตมาตามีพื้นฐานมาจากแนวคิดทางคณิตศาสตร์ที่แม่นยำซึ่งทำให้เกิดแนวคิดที่เข้าใจง่ายเกี่ยวกับการทำงาน (พฤติกรรม) ของออโตมาตอนและเกี่ยวกับโครงสร้าง (โครงสร้างภายใน)

ในกรณีนี้ การแปลงข้อมูลมักจะเข้าใจว่าเป็นการดำเนินการที่แปลงลำดับอินพุตที่ประกอบด้วยตัวอักษรจากตัวอักษรอินพุตเป็นลำดับเอาต์พุตที่ประกอบด้วยตัวอักษรจากตัวอักษรเอาต์พุต

เครื่องมือของตรรกะทางคณิตศาสตร์ พีชคณิต ทฤษฎีความน่าจะเป็น combinatorics และทฤษฎีกราฟถูกนำมาใช้กันอย่างแพร่หลาย

ปัญหาเกี่ยวกับทฤษฎีของออโตมาตะในบางส่วนของมัน (ทฤษฎีโครงสร้างของออโตมาตา) ได้เติบโตขึ้น จากทฤษฎีวงจรหน้าสัมผัสรีเลย์ซึ่งเริ่มเป็นรูปเป็นร่างในช่วงปลายทศวรรษที่ 1930 รวม วิธีการของพีชคณิตเชิงตรรกะ.

ในทฤษฎีโครงสร้างของออโตมาตา มีการศึกษาโครงร่างประเภทต่างๆ ซึ่งออกแบบมาเพื่ออธิบายว่าหุ่นยนต์ที่ซับซ้อนถูกสร้างขึ้นจากส่วนประกอบ (องค์ประกอบ) ที่ง่ายกว่าซึ่งเชื่อมต่ออย่างเหมาะสมในระบบอย่างไร

อีกทิศทางหนึ่งเรียกว่าทฤษฎีนามธรรมของออโตมาตะ ศึกษาพฤติกรรมของออโตมาตะ (นั่นคือธรรมชาติของการเปลี่ยนแปลงของข้อมูลที่ดำเนินการโดยพวกเขา) ในขณะที่แยกออกจากโครงสร้างภายในที่เฉพาะเจาะจงและเกิดขึ้นในปี 1950

ภายในกรอบของทฤษฎีเชิงนามธรรมของออโตมาตา เนื้อหาของแนวคิด "ออโตมาตอน" และ "เครื่องจักร" นั้นหมดลงโดยพื้นฐานแล้วโดยคำอธิบายมาตรฐานของการเปลี่ยนแปลงข้อมูลที่ดำเนินการโดยออโตมาตอน การเปลี่ยนแปลงดังกล่าวสามารถกำหนดได้ แต่ก็มีความเป็นไปได้ในธรรมชาติเช่นกัน

การศึกษาส่วนใหญ่คือเครื่องจักรเชิงกำหนด (ออโตมาตา) ซึ่งรวมถึงออโตมาตาที่มีจำกัด ซึ่งเป็นเป้าหมายหลักของการศึกษาในทฤษฎีออโตมาตา

เครื่องสถานะจำกัดมีลักษณะเป็นหน่วยความจำจำนวนจำกัด (จำนวนสถานะภายใน) และถูกกำหนดโดยใช้ฟังก์ชันการเปลี่ยนแปลงด้วยอุดมคติที่สมเหตุสมผล เครื่องจักรทางคณิตศาสตร์สมัยใหม่ทั้งหมดและแม้แต่สมอง จากมุมมองของการทำงานของมัน ถือได้ว่าเป็นออโตมาตาที่มีขอบเขตจำกัด

คำว่า "sequential machine", "Milly automaton", "Moore automaton" ใช้ในวรรณกรรม (และไม่เหมือนกันโดยผู้เขียนทุกคน) เป็นคำพ้องของคำว่า "finite automaton" หรือเพื่อเน้นคุณลักษณะบางอย่างในฟังก์ชันการเปลี่ยนแปลงของ finite หุ่นยนต์

ออโตมาตาที่มีหน่วยความจำไม่จำกัดเป็นเครื่องทัวริงที่สามารถดำเนินการ (อาจ) แปลงข้อมูลอย่างมีประสิทธิภาพ แนวคิดของ "เครื่องจักรทัวริง" เกิดขึ้นก่อนแนวคิดของ "เครื่องจักรสถานะจำกัด" และส่วนใหญ่ศึกษาในทฤษฎีอัลกอริทึม

ทฤษฎีออโตมาตาที่เป็นนามธรรมมีความเกี่ยวข้องอย่างใกล้ชิดกับทฤษฎีเกี่ยวกับพีชคณิตที่รู้จักกันดี ตัวอย่างเช่น ทฤษฎีเซมิกรุ๊ป จากมุมมองที่ใช้ ผลลัพธ์ที่แสดงลักษณะของการเปลี่ยนแปลงข้อมูลในหุ่นยนต์ในแง่ของขนาดหน่วยความจำเป็นที่สนใจ

ในกรณีนี้ ตัวอย่างเช่น ในปัญหาเกี่ยวกับการทดลองเกี่ยวกับออโตมาตา (งานของ E.F. Moore เป็นต้น) โดยที่ข้อมูลอย่างใดอย่างหนึ่งเกี่ยวกับฟังก์ชันการเปลี่ยนแปลงของออโตมาตอนหรือเกี่ยวกับความจุของหน่วยความจำนั้นได้มาจากผลลัพธ์ของ การทดลอง

อีกงานหนึ่งคือการคำนวณระยะเวลาของลำดับเอาต์พุต ตามข้อมูลที่มีอยู่เกี่ยวกับขนาดหน่วยความจำของหุ่นยนต์และระยะเวลาของลำดับอินพุต

สิ่งสำคัญอย่างยิ่งคือการพัฒนาวิธีการลดหน่วยความจำของเครื่องจักรสถานะจำกัดและศึกษาพฤติกรรมของพวกมันในสภาพแวดล้อมสุ่ม

ในทฤษฎีออโตมาตาเชิงนามธรรม ปัญหาการสังเคราะห์มีดังต่อไปนี้ในแง่ของภาษาที่เป็นทางการอย่างชัดเจน เงื่อนไขจะถูกเขียนขึ้นสำหรับพฤติกรรมของหุ่นยนต์ที่ออกแบบ (สำหรับเหตุการณ์ที่แสดงในหุ่นยนต์) ในกรณีนี้จำเป็นต้องพัฒนาวิธีการตามเงื่อนไขที่เป็นลายลักษณ์อักษรแต่ละข้อ:

1) ค้นหาว่ามีเครื่องสถานะดังกล่าวอยู่หรือไม่ซึ่งข้อมูลที่แปลงโดยมันตรงตามเงื่อนไขนี้

2) ถ้าใช่ ฟังก์ชันการเปลี่ยนสถานะของเครื่องสถานะจำกัดดังกล่าวจะถูกสร้างขึ้นหรือประมาณขนาดหน่วยความจำของมัน

วิธีแก้ปัญหาของงานสังเคราะห์ในสูตรดังกล่าวสันนิษฐานว่าการสร้างเบื้องต้นของภาษาที่สะดวกสำหรับการบันทึกเงื่อนไขการทำงานของหุ่นยนต์ด้วยอัลกอริทึมที่สะดวกสำหรับการเปลี่ยนจากการบันทึกเป็นฟังก์ชันสกรรมกริยา

ในทฤษฎีโครงสร้างของออโตมาตา ปัญหาการสังเคราะห์ประกอบด้วยการสร้างสายโซ่ขององค์ประกอบตามประเภทที่กำหนดซึ่งทำให้เกิดออโตมาตอนจำกัดที่กำหนดโดยฟังก์ชันการเปลี่ยนผ่านของมัน ในกรณีนี้ พวกเขามักจะระบุเกณฑ์ความเหมาะสมบางประการ (เช่น จำนวนองค์ประกอบขั้นต่ำ) และพยายามให้ได้โครงร่างที่เหมาะสมที่สุด

เมื่อปรากฎในภายหลัง หมายความว่าวิธีการและแนวคิดบางอย่างที่พัฒนาขึ้นก่อนหน้านี้เกี่ยวกับวงจรหน้าสัมผัสรีเลย์ใช้ได้กับวงจรประเภทอื่น

ในการเชื่อมต่อกับการพัฒนาเทคโนโลยีอิเล็กทรอนิกส์รูปแบบที่แพร่หลายที่สุดคือ ขององค์ประกอบการทำงาน (เครือข่ายเชิงตรรกะ). กรณีพิเศษของเครือข่ายลอจิกคือโครงข่ายประสาทเทียมแบบนามธรรม ซึ่งมีองค์ประกอบที่เรียกว่าเซลล์ประสาท

มีการพัฒนาวิธีการสังเคราะห์หลายวิธีขึ้นอยู่กับประเภทของวงจรและการแปลงข้อมูลที่ต้องการ (การสังเคราะห์อุปกรณ์รีเลย์)

ดู -การย่อวงจรเชิงผสม แผนที่การ์โนต์ การสังเคราะห์วงจร

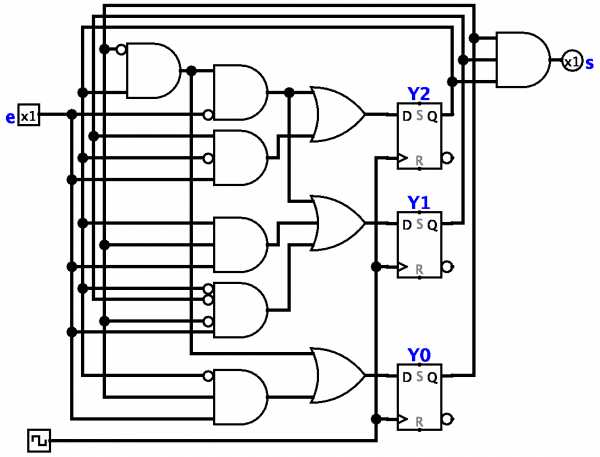
เครื่องสถานะจำกัด — แบบจำลองทางคณิตศาสตร์ของระบบควบคุมที่มีขนาดหน่วยความจำคงที่ (ไม่สามารถเพิ่มได้ระหว่างการทำงาน)

แนวคิดของเครื่องจักรสถานะจำกัดคือนามธรรมทางคณิตศาสตร์ที่แสดงลักษณะทั่วไปของชุดระบบควบคุม (ตัวอย่างเช่น อุปกรณ์รีเลย์แบบมัลติลูป) ระบบดังกล่าวทั้งหมดมีคุณสมบัติทั่วไปที่ยอมรับได้ตามธรรมชาติว่าเป็นคำจำกัดความของออโตเมตอนที่มีขอบเขตจำกัด

เครื่องจักรที่สร้างเสร็จแล้วทุกเครื่องมีทางเข้าที่เปิดรับอิทธิพลจากภายนอกและองค์ประกอบภายใน สำหรับทั้งอินพุตและองค์ประกอบภายใน มีจำนวนสถานะที่ไม่ต่อเนื่องที่แน่นอนที่สามารถใช้

การเปลี่ยนแปลงสถานะของอินพุตและองค์ประกอบภายในเกิดขึ้นในช่วงเวลาที่ไม่ต่อเนื่องกัน ช่วงเวลาระหว่างนั้นเรียกว่า ขีด สถานะภายใน (สถานะภายใน) ที่ส่วนท้ายของเทปถูกกำหนดโดยสถานะภายในทั้งหมดและสถานะของอินพุตที่จุดเริ่มต้นของเทป

นิยามอื่นๆ ทั้งหมดของออโตมาตอนแบบจำกัดสามารถลดลงเป็นคุณลักษณะนี้ โดยเฉพาะคำจำกัดความที่ถือว่าออโตมาตอนแบบจำกัดมีเอาต์พุตที่ขึ้นอยู่กับสถานะภายในของออโตมาตอน ณ เวลาที่กำหนด

ในแง่ของลักษณะดังกล่าว ลักษณะของอินพุตและสถานะภายในนั้นไม่เกี่ยวข้องกับคำอธิบายของหุ่นยนต์ที่สมบูรณ์ แทนที่จะเป็นอินพุตและสถานะ คุณสามารถดูตัวเลขได้ด้วยการสุ่มตัวเลข

เครื่องสถานะจะถูกตั้งค่าหากมีการระบุการพึ่งพาหมายเลขสถานะภายในกับหมายเลขสถานะภายในก่อนหน้าและระบุหมายเลขสถานะอินพุตก่อนหน้า งานดังกล่าวสามารถอยู่ในรูปแบบของตารางสุดท้าย

อีกวิธีทั่วไปในการกำหนดหุ่นยนต์ที่สมบูรณ์คือการสร้างสิ่งที่เรียกว่า แผนภาพการเปลี่ยนแปลง สถานะอินพุตมักเรียกง่ายๆ ว่าอินพุต และสถานะภายในคือสถานะง่ายๆ

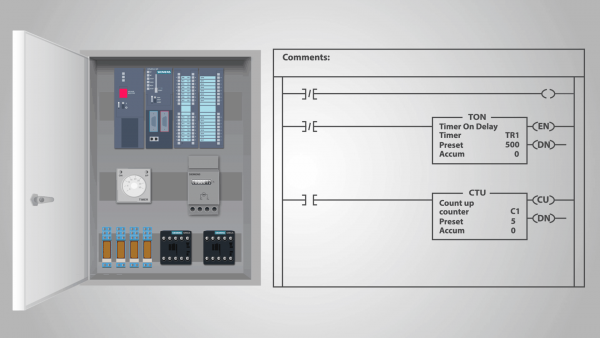
เครื่องสถานะจำกัดสามารถเป็นแบบจำลองของทั้งอุปกรณ์ทางเทคนิคและระบบทางชีววิทยาบางอย่าง ออโตมาตะประเภทแรก ได้แก่ อุปกรณ์รีเลย์และคอมพิวเตอร์อิเล็กทรอนิกส์ต่างๆ รวมถึง ตัวควบคุมลอจิกที่ตั้งโปรแกรมได้.

ในกรณีของอุปกรณ์รีเลย์ บทบาทของสถานะอินพุตจะเล่นโดยการรวมกันของสถานะขององค์ประกอบที่ละเอียดอ่อนของอุปกรณ์รีเลย์ (การรวมกันของสถานะดังกล่าวแต่ละสถานะคือ «สถานะที่ซับซ้อน» ซึ่งแสดงลักษณะเฉพาะด้วยการบ่งชี้องค์ประกอบที่ละเอียดอ่อนทั้งหมดของ สถานะที่ไม่ต่อเนื่องเหล่านี้ที่พวกเขามีในช่วงเวลาที่กำหนด) ในทำนองเดียวกัน การรวมกันของสถานะขององค์ประกอบระดับกลางของอุปกรณ์รีเลย์จะทำหน้าที่เป็นสถานะภายใน

ตัวควบคุมลอจิกที่ตั้งโปรแกรมได้ (PLC) เป็นตัวอย่างของอุปกรณ์การดำเนินการรีเลย์ที่สามารถเรียกว่าเครื่องสถานะสแตนด์อโลน

ในความเป็นจริง เมื่อโปรแกรมถูกป้อนเข้าไปใน PLC และตัวควบคุมได้เริ่มทำการคำนวณ โปรแกรมจะไม่ได้รับอิทธิพลจากภายนอก และแต่ละสถานะที่ตามมาจะถูกกำหนดโดยสถานะก่อนหน้าอย่างสมบูรณ์ เราสามารถสันนิษฐานได้ว่าอินพุตมีสถานะเดียวกันในทุกรอบสัญญาณนาฬิกา

ในทางกลับกัน เครื่องจักรสถานะจำกัดใด ๆ ที่มีสถานะอินพุตเดียวที่เป็นไปได้โดยธรรมชาติเรียกว่าเป็นอิสระ เนื่องจากในกรณีนี้ สภาพแวดล้อมภายนอกไม่มีข้อมูลที่ควบคุมพฤติกรรมของมัน

ดูสิ่งนี้ด้วย:

การใช้ระบบไมโครโปรเซสเซอร์ในงานวิศวกรรมไฟฟ้า ตัวอย่างการใช้ PLC

โลโก้โมดูลลอจิก! สำหรับระบบอัตโนมัติทางอุตสาหกรรม